【過去問解答】2022年統計検定1級＜数理統計問1＞

統計検定1級の過去問解答解説を行います。目次は以下をご覧ください。

不適切な内容があれば，記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。

問題

統計検定1級の過去問からの出題になります。統計検定の問題の著作権は日本統計学会に帰属していますので，本稿にて記載することはできません。「演習問題を俯瞰する」で詳しく紹介している公式の過去問題集をご購入いただきますようお願い致します。

解答

確率空間と事象に関する出題でした。過去にない傾向の内容であったため，戸惑った受験生も多かったように思えます。

(1)

独立の定義より，$P(A\cap B)$は

と求められます。同様に，$P(A\cap B\cap C)$は

と求められます。

補足

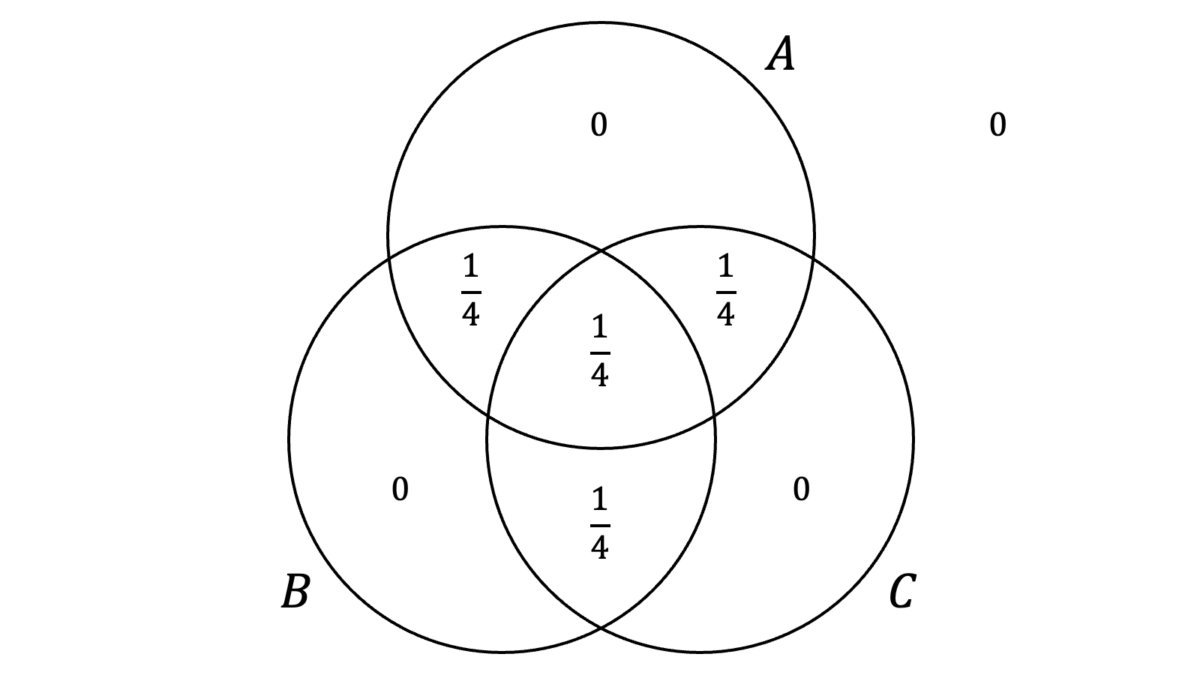
小問(1)のベン図は下記のようになります。

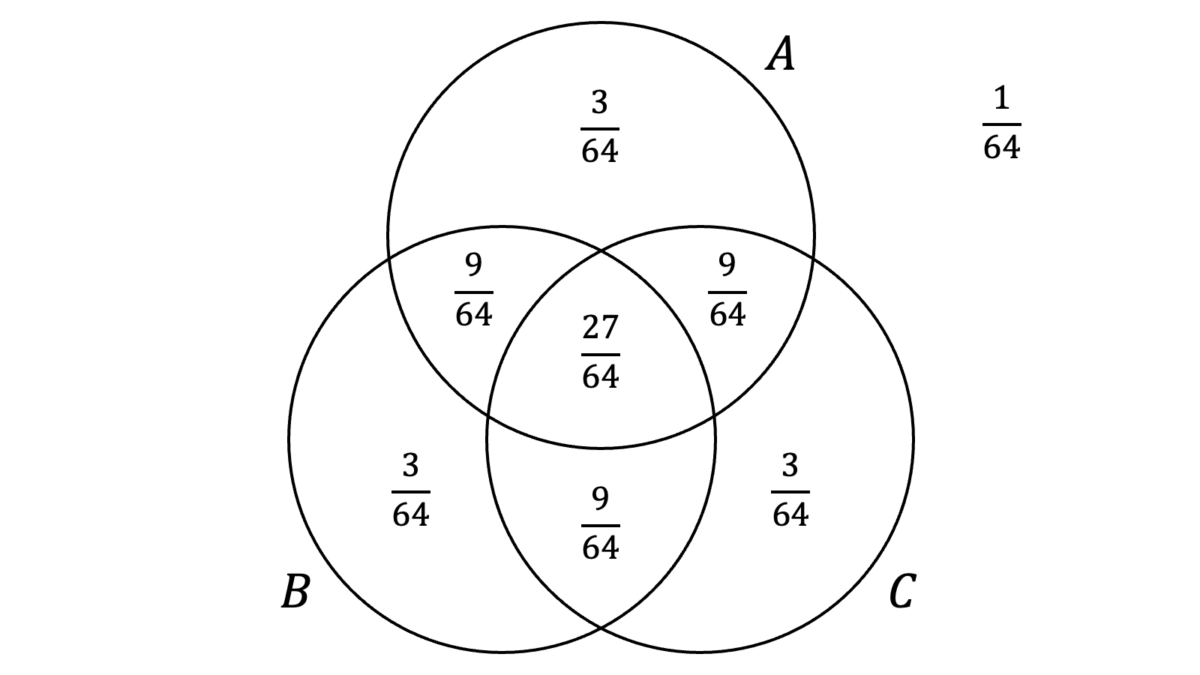
(2)

$P(A\cap B)$は$P(A\cup B)$を用いて

と表されますので，$P(A\cup B)$が最小のときに$P(A\cap B)$は最大となり，$P(A\cup B)$が最大のときに$P(A\cap B)$は最小となります。$P(A\cup B)$が最小となるのは，ベン図において$A$と$B$ができるだけ一致する場合であり，$A{=}B$のときです。

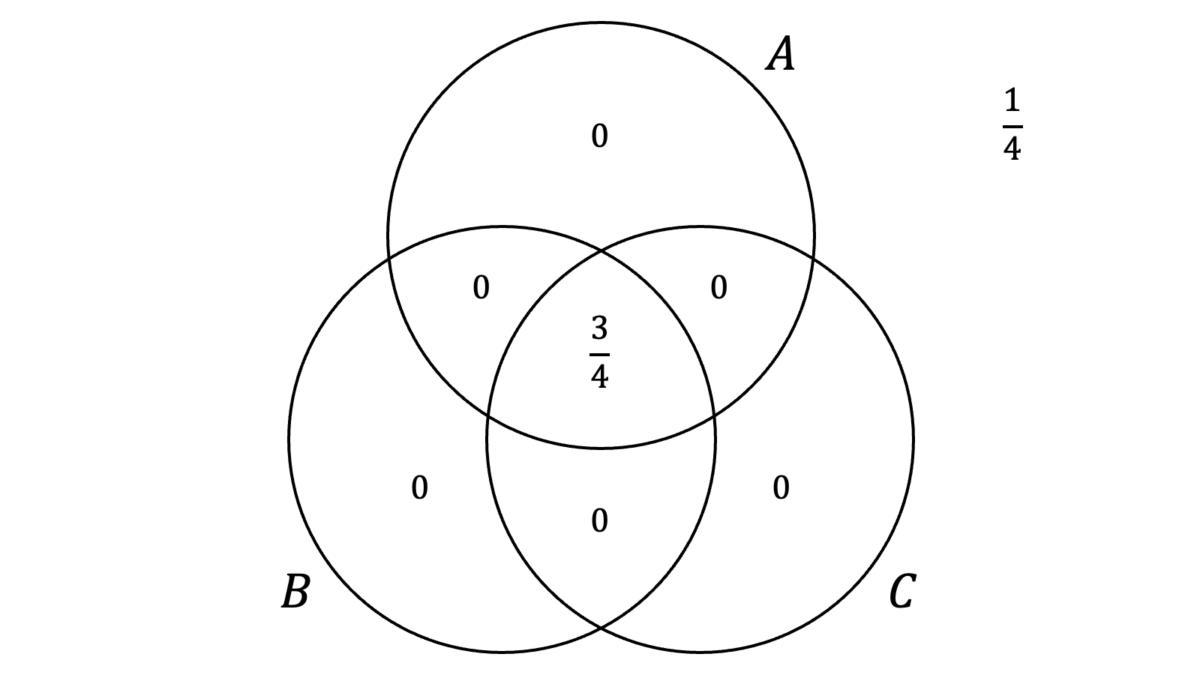
したがって，$P(A\cup B){=}3/4$となるため，

となります。一方，$P(A\cup B)$が最大となるのは，ベン図において$A$と$B$ができるだけ離れる場合であり，$A\cup B$が全事象$\Omega$と一致するときです。

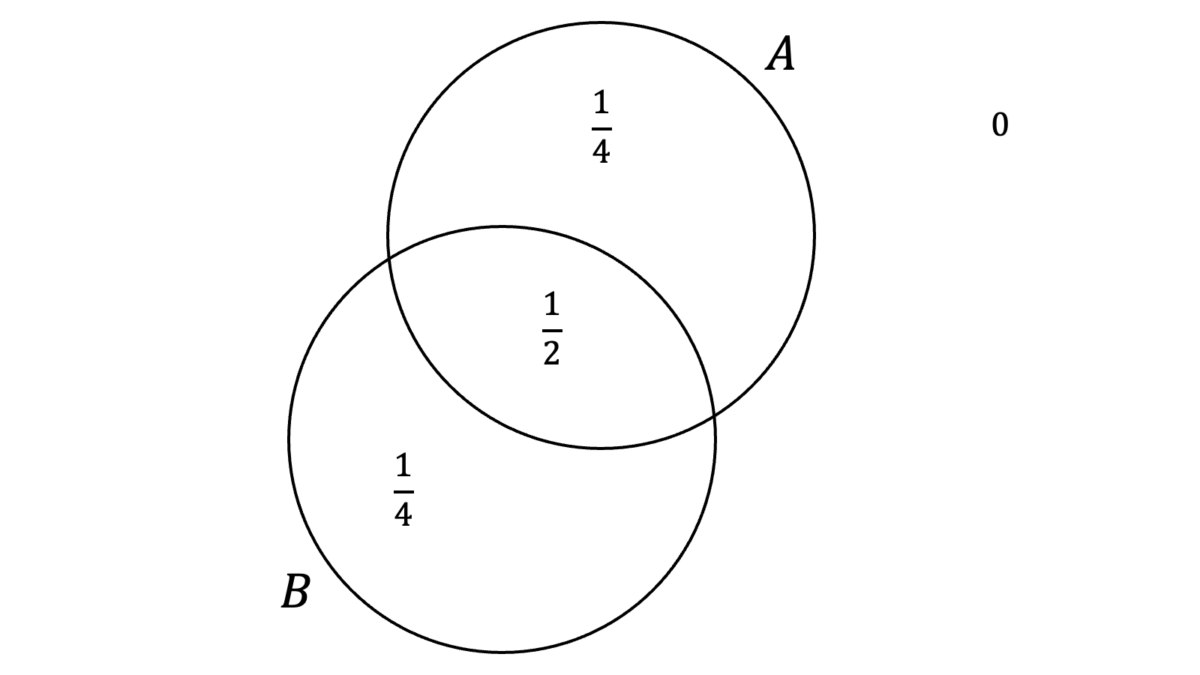
したがって，$P(A\cup B){=}1$となるため，

となります。以上より

が得られます。

(3)

前問と同様に考えます。$P(A\cap B\cap C)$は$P(A\cup B)$，$P(B\cup C)$，$P(C\cup A)$を用いて

と表されます。一般に，$P(A\cup B)$，$P(B\cup C)$，$P(C\cup A)$の三つが定まっても$P(A\cup B\cup C)$は定まりませんので，$P(A\cup B)$，$P(B\cup C)$，$P(C\cup A)$が最小かつ$P(A\cup B\cup C)$が最大のときに$P(A\cap B\cap C)$は最大となり，$P(A\cup B)$，$P(B\cup C)$，$P(C\cup A)$が最大かつ$P(A\cup B\cup C)$が最小のときに$P(A\cap B\cap C)$は最小となります。さて，$P(A\cup B)$，$P(B\cup C)$，$P(C\cup A)$が最小となるのは，ベン図において$A$と$B$と$C$ができるだけ一致する場合であり，$A{=}B{=}C$のときです。

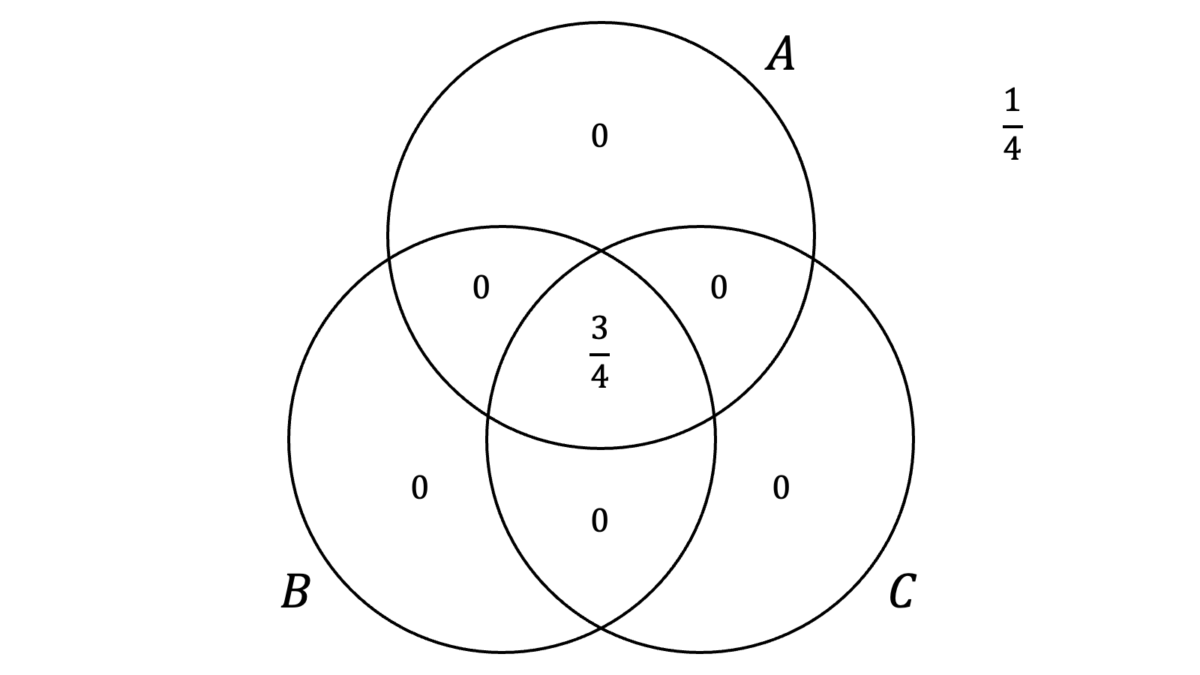
このとき，$P(A\cup B)$，$P(B\cup C)$，$P(C\cup A)$はいずれも$3/4$となりますが，$P(A\cup B\cup C)$も一意に定まり，$3/4$となります。したがって，

となります。一方，$P(A\cup B)$，$P(B\cup C)$，$P(C\cup A)$が最大となるのは，ベン図において$A$と$B$と$C$ができるだけ離れる場合であり，$A\cup B$，$B\cup C$，$C\cup A$が全事象$\Omega$と一致するときです。

このとき，$P(A\cup B)$，$P(B\cup C)$，$P(C\cup A)$はいずれも$1$となりますが，余事象$P(A\cup B\cup C)$も一意に定まり，$1$となります。したがって，

となります。したがって，

が得られます。

(4)

この問題は$3$変数の独立の概念が理解できているかどうかを問う問題です。上でも和集合の場合で述べましたが，一般に$P(A\cap B)$，$P(B\cap C)$，$P(C\cap A)$の三つが定まっても$P(A\cap B\cap C)$は定まりません。別の言葉で表現すれば，$(A,B)$，$(B,C)$，$(C,A)$がそれぞれ独立でも，$(A,B,C)$が独立とは限りません。つまり，問題文で与えられている条件だけでは，$P(A\cap B\cap C)$は一意に定まらないということです。与えられた条件より，小問(2)と同様にして

が得られます。同様に，$P(B\cup C){=}P(C\cup A){=}15/16$が得られます。よって，小問(3)と同様にして

となります。よって，$P(A\cup B\cup C)$が最小のときに$P(A\cap B\cap C)$は最小となり，$P(A\cup B\cup C)$が最大のときに$P(A\cap B\cap C)$は最大となります。$P(A\cup B\cup C)$が最小となるのは，$A$と$B$と$C$ができるだけ一致する場合です。しかし，前問とは異なり$P(A\cup B){=}P(B\cup C){=}P(C\cup A){=}15/16$であることから，$A{=}B{=}C$とはなり得ません。したがって，「$A,B,C$だけが固有に有する確率」を最小化して$0$とすることを考えます。

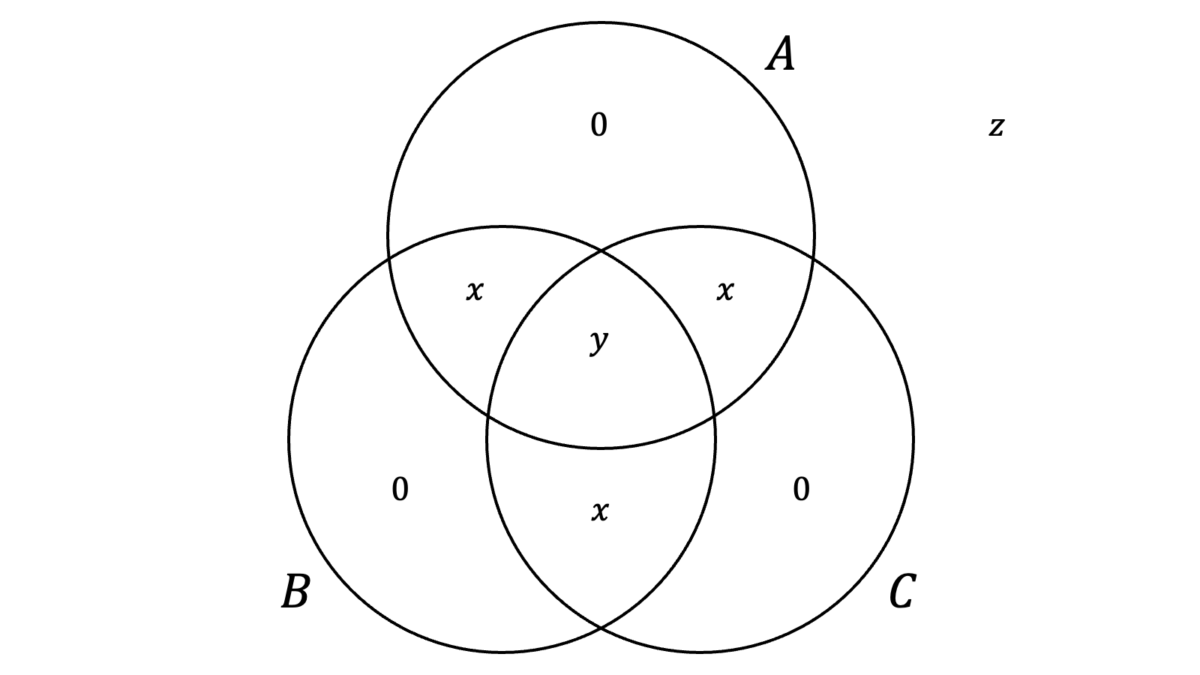
図中の$x,y,z$について

\begin{cases}
\displaystyle
3x + y + z = 1 \\[0.7em]
\displaystyle
3x + y = \frac{15}{16}\\[0.7em]
\displaystyle
2x + y = \frac{3}{4}
\end{cases}

が成り立つため，$(x,y,z){=}(3/16,3/8,1/16)$となります。$P(A\cup B\cup C){=}15/16$となるため，

となります。一方，$P(A\cup B\cup C)$が最大となるのは，ベン図において$A$と$B$と$C$ができるだけ離れる場合です。したがって，「$A,B,C$以外が有する確率」を$0$とすれば$A,B,C$が最も離れますので，下記のようなベン図を考えます。

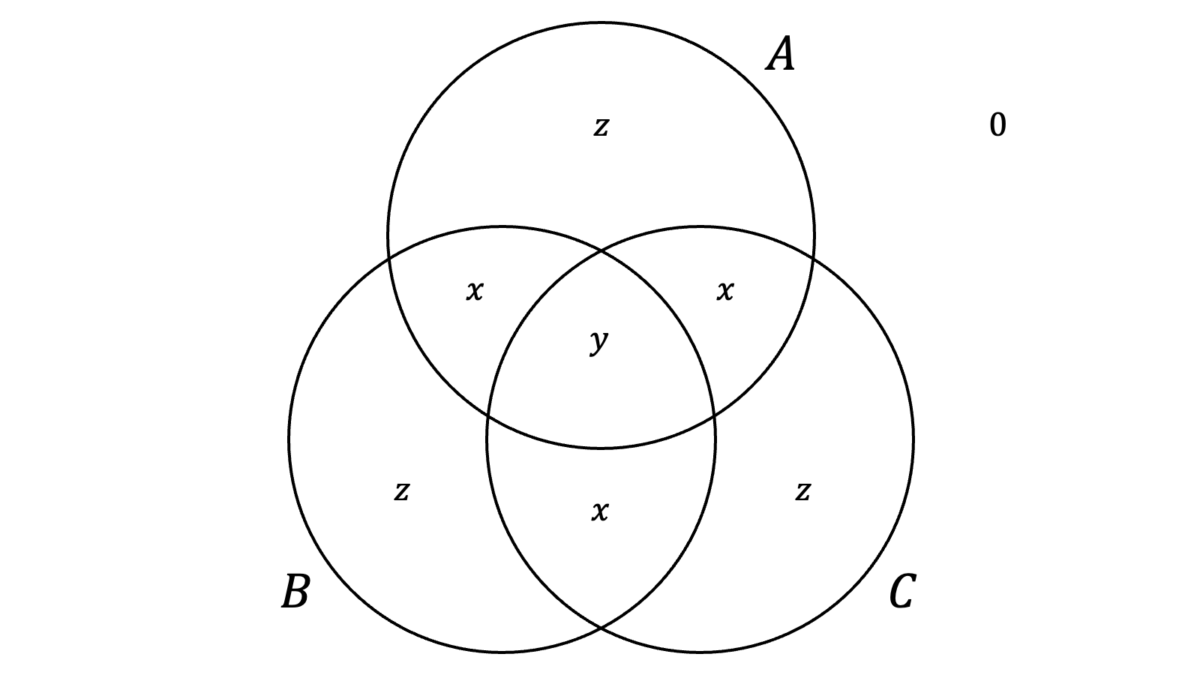
図中の$x,y,z$について

\begin{cases}
\displaystyle
3x + 3y + z = 1\\[0.7em]
\displaystyle
2x + 3y + z = \frac{15}{16}\\[0.7em]
\displaystyle
x + 2y + z = \frac{3}{4}
\end{cases}

が成り立つため，$(x,y,z){=}(1/16,1/8,7/16)$となります。$P(A\cup B\cup C){=}1$となるため，

となります。

連立方程式を解くまでもなく，ベン図より$P(A\cup B\cup C){=}1$が分かります。