統計検定1級の過去問解答解説を行います。目次は以下をご覧ください。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
問題
統計検定1級の過去問からの出題になります。統計検定の問題の著作権は日本統計学会に帰属していますので,本稿にて記載することはできません。「演習問題を俯瞰する」で詳しく紹介している公式の過去問題集をご購入いただきますようお願い致します。
解答
棄却域と一様最強力検定に関する出題でした。
(1)
- $\barx=0.3$のときの$P$-値:$0.17$
- $\barx=0.6$のときの$P$-値:$0.03$
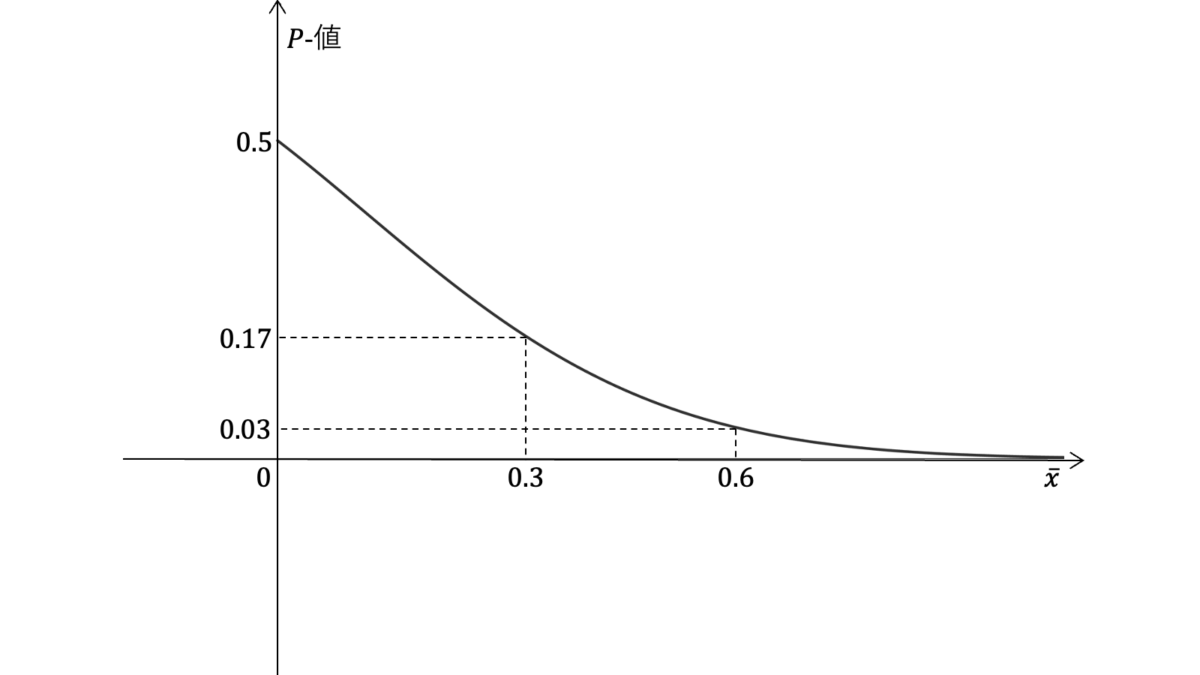
棄却域の判定に標準正規分布を仮定しているため,標準正規分布の確率密度関数$f(x)$に対して分布関数を
\Phi(z) &= \int_{-\infty}^{z}f(x)dx
\end{align}
とおきます。$\barX$は$\N(0,1/n)$に従い,$U\sim\N(0,1/n)$に対し$\sqrt{n}U$は標準正規分布に従うことに注意すると,$P$-値は
P(U\geq\barx)
&= P(\sqrt{n}U\geq\sqrt{n}\barx)
= P(Z\geq\sqrt{n}\barx)
= 1-\Phi(\sqrt{n}\barx)
\end{align}
と求められます。ただし,$Z\sim\N(0,1)$としました。正規分布の分布関数表を用いて$\barx{=}0.3,0.6$と端点の$P$-値を調べると,下表のようになります。
| $n$ | $\barx$ | $\Phi(\sqrt{n}\barx)$ | $P$-値 |
|---|---|---|---|
| $10$ | $0$ | $0.5$ | $0.5$ |
| $10$ | $0.3$ | $0.83$ | $0.17$ |
| $10$ | $0.6$ | $0.97$ | $0.03$ |
| $10$ | $\infty$ | $1$ | $0$ |
標準正規分布の上側確率表が与えられている場合は,$\Phi(z)$を経由せずに直接$P$-値を求めてもよいです。
$\Phi(z)$が単調増加関数で$P$-値は単調減少関数となることに注意すると,上のグラフを描くことができます。
(2)
前問(1)より,$P$-値は$1-\Phi(\sqrt{n}\barx)$と求められる。この$P$-値が$\alpha$より小さくなるときは,
\sqrt{n}\barx > z_{\alpha}
\end{align}
を満たすため,$\barx>z_{\alpha}/\sqrt{n}$を満たす。すなわち,$\barx$が棄却域に落ちることと同等である。
(3)
- $(n,\mu)=(9,0.4)$のとき,検出力は$0.33$
- $(n,\mu)=(9,0.8)$のとき,検出力は$0.77$
- $(n,\mu)=(16,0.4)$のとき,検出力は$0.48$
- $(n,\mu)=(16,0.8)$のとき,検出力は$0.94$
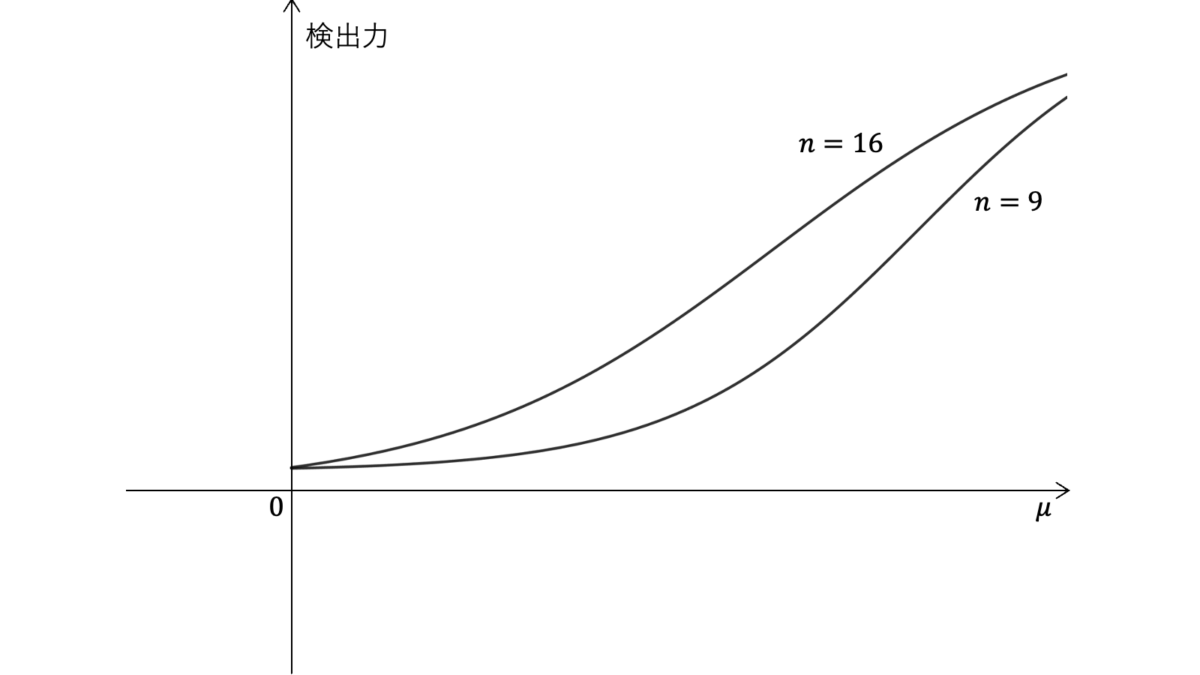
$\barX\sim\N(\mu,1/n)$に対し棄却域は$\barX>z_{\alpha}/\sqrt{n}$であることから,第二種の過誤を犯す確率を$\beta$とおくと,検出力は
1-\beta
&= 1{-}P\left(\barX\leq \frac{z_{\alpha}}{\sqrt{n}}\right)
= P\left(\barX>\frac{z_{\alpha}}{\sqrt{n}}\right)
= P\left(\frac{\barX-\mu}{1/\sqrt{n}}>\frac{z_{\alpha}}{\sqrt{n}/\sqrt{n}}-\frac{\mu}{1/\sqrt{n}}\right)\\[0.7em]
&= P\left(Z>z_{\alpha}-\sqrt{n}\mu\right)
\end{align}
と表されます。$z_{0.05}=1.645$に注意すると,下表が得られます。
| $n$ | $\mu$ | 検出力 |
|---|---|---|
| $9$ | $0.4$ | $P(Z>1.645-0.4\cdot 3)=P(Z>0.445)=0.33$ |
| $9$ | $0.8$ | $P(Z>1.645-0.8\cdot 3)=P(Z>-0.755)=1-0.23=0.77$ |
| $16$ | $0.4$ | $P(Z>1.645-0.4\cdot 4)=P(Z>0.045)=0.48$ |
| $16$ | $0.8$ | $P(Z>1.645-0.8\cdot 4)=P(Z>-19555)=1-0.06=0.94$ |
検出力が$\mu$の単調増加関数であること,および上表を参考にすると,解答のグラフを描くことができます。
(4)
$z_{0.2}=0.842$であることに注意すると,題意を満たす$n$は
1.645-0.5\sqrt{n} < -0.842
\end{align}
を満たす。これを変形すると$\sqrt{n}>(1.645+0.842)\cdot 2=4.974$となるため,$n\geq 25$が得られる。
(5)
帰無仮説$H_{0}:\mu=0$の対立仮説$H_{1}:\mu=\mu_{1}$に対する最強力検定は,$\vx=(x_{1},\ldots,x_{n})$の同時確率密度関数と定数$c$を用いて
\frac{f(\vx;\mu_{1})}{f(\vx;0)}>c\label{5_1}
\end{align}
の形となる。左辺は
\exp\left\{{-}\frac{\sum_{i=1}^{n}(x_{i}-\mu_{1})^{2}}{2}+\frac{\sum_{i=1}^{n}x_{i}^{2}}{2}\right\}
= \exp\left(\mu_{1}\sum_{i=1}^{n}x_{i}{-}\frac{n\mu_{1}^{2}}{2}\right)
= \exp\left\{n\mu_{1}\left(\barx{-}\frac{\mu_{1}}{2}\right)\right\}
\end{align}
と表され,$n>0$かつ$\mu_{1}>0$であることから,式($\ref{5_1}$)の形となるためには$\barx>c^{\prime}$となる。$c^{\prime}$として$z_{\alpha}/\sqrt{n}$を選んだ場合,小問(2)より$P$-値が$\alpha$より小さくなることと$\barx$が棄却域に落ちることは同等となるため,この検定が有意水準$\alpha$のもとで帰無仮説$H_{0}$と対立仮説$H_{1}$に対する最強力検定となることが示される。また,$c^{\prime}$が$\mu_{1}$に依存しないため,この検定は一様最強力検定となる。


コメント