本記事は数学の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
目次
基底変換行列の逆行列
$V$を$\mK$上の$n$次元ベクトル空間とし,$\alpha,\alpha^{\prime}$を$V$の二つの基底とする。このとき,基底変換行列$\mT_{\alpha\rightarrow\alpha^{\prime}}$は$n$次の正則行列で,その逆行列は
\begin{align}
P^{-1} &= \mT_{\alpha^{\prime}\rightarrow\alpha}
\end{align}
P^{-1} &= \mT_{\alpha^{\prime}\rightarrow\alpha}
\end{align}
である。
基底変換行列の定義より自然に導かれる定理です。
証明
$\varphi$が同型写像であることから$\varphi_{\alpha^{\prime}}$には逆写像が存在することに注意すると,基底変換行列を定める変換$L_{P}=\varphi_{\alpha}^{-1}\circ\varphi_{\alpha^{\prime}}$の逆変換は
\begin{align}
L^{-1}_{P} &= \varphi_{\alpha^{\prime}}^{-1}\circ\varphi_{\alpha}
\end{align}
L^{-1}_{P} &= \varphi_{\alpha^{\prime}}^{-1}\circ\varphi_{\alpha}
\end{align}
となります。すなわち,基底変換行列の逆行列は$\mT_{\alpha^{\prime}\rightarrow\alpha}$と等しくなります。これは,可視化して考えると分かりやすいです。基底変換行列の定義でみたように,$L^{-1}_{P}$は下図の通りに表されます。
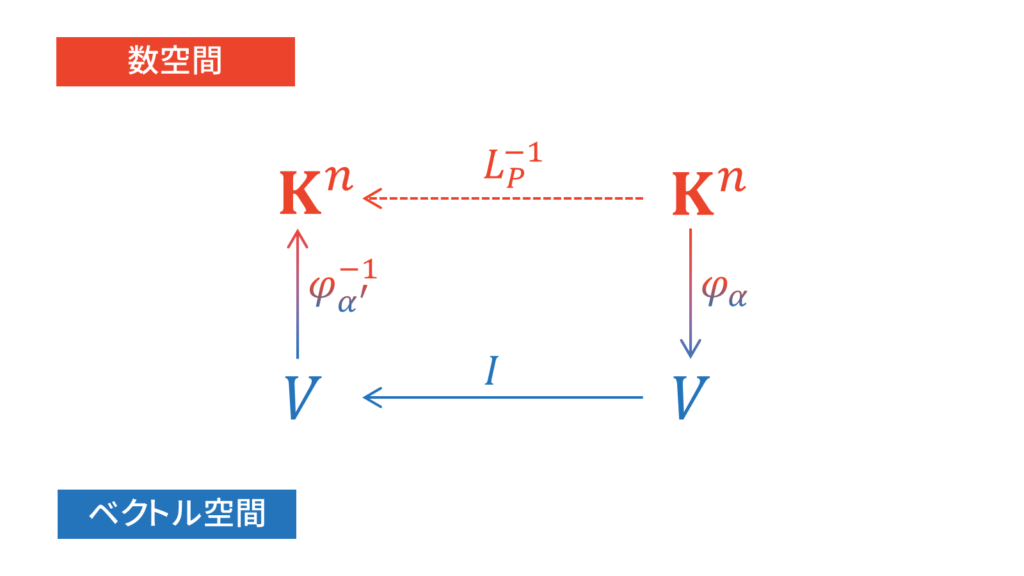
$L^{-1}_{P}$は恒等写像$I:V\rightarrow V$の基底$\alpha,\alpha^{\prime}$に関する表現行列$[I]_{\alpha^{\prime}}^{\alpha}$に等しく,したがって$\mT_{\alpha\rightarrow\alpha^{\prime}}$の逆行列は$\mT_{\alpha^{\prime}\rightarrow\alpha}$となることが分かります。


コメント