本記事は数学の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
目次
基底変換行列
$V$を$\mK$上の$n$次元ベクトル空間とし,
\begin{align}
\alpha=\{v_{1},\ldots,v_{n}\},\quad\alpha^{\prime}=\{v^{\prime}_{1},\ldots,v^{\prime}_{n}\}
\end{align}
\alpha=\{v_{1},\ldots,v_{n}\},\quad\alpha^{\prime}=\{v^{\prime}_{1},\ldots,v^{\prime}_{n}\}
\end{align}
を$V$の二つの基底とする。このとき,
\begin{align}
\varphi_{\alpha}^{-1}\circ\varphi_{\alpha} &= L_{P}
\end{align}
\varphi_{\alpha}^{-1}\circ\varphi_{\alpha} &= L_{P}
\end{align}
によって定義される$n$次正方行列$P$を,$\alpha$から$\alpha^{\prime}$への基底変換行列といい,記号$\mT_{\alpha\rightarrow\alpha^{\prime}}$で表す。ただし,$\varphi$は同型写像を表す。
恒等写像の異なる基底に関する表現行列を基底変換行列といいます。
補足1
$V$の恒等変換を$I$とおけば,下図の通り$\varphi_{\alpha}^{-1}\circ\varphi_{\alpha}$は$\varphi_{\alpha}^{-1}\circ I\circ\varphi_{\alpha}$と書けます。
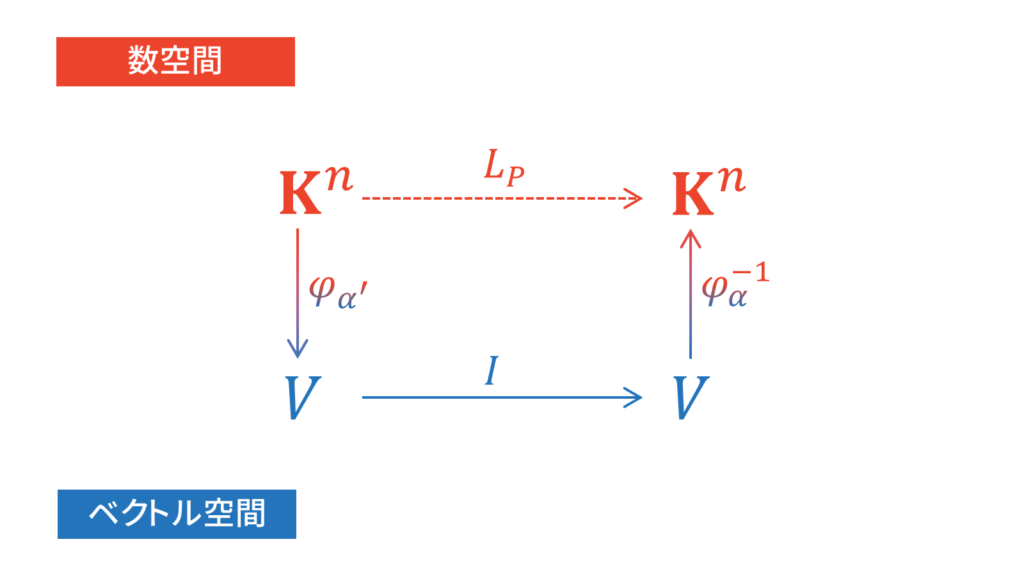
したがって,$\mT_{\alpha\rightarrow\alpha^{\prime}}$は恒等写像$I:V\rightarrow V$の基底$\alpha^{\prime},\alpha$に関する表現行列$[I]_{\alpha}^{\alpha^{\prime}}$に等しくなります。それゆえ,表現行列の定義より,$j{=}1,\ldots,n$に対し
\begin{align}
v^{\prime}_{j} &= \sum_{i=1}^{n}p_{ij}v_{i}
\end{align}
v^{\prime}_{j} &= \sum_{i=1}^{n}p_{ij}v_{i}
\end{align}
が成り立ちます。
補足2
基底変換行列は$n$個の基底から$n$個の基底に変換する行列ですから,行空間の次元と列空間の次元はともに$n$となります。ゆえに,基底変換行列はフルランクですので正則になります。したがって,基底変換行列は「正則な線型変換を施す行列」ということもできます。


コメント