本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
この記事の流れ
まずは相関関係と因果関係の包含関係を確認します。さらに,確率変数を条件付けることがある因子を特定の状態に固定することを意味していることに注目します。
簡単のためアスタリスク$\ast$を用いた新しい確率変数を導入します。
相関と回帰の違いを「条件付けられているかどうか」という視点を通して俯瞰してみます。
相関係数を考えるときに「データの母集団に正規分布を仮定すべきだ派閥」と「最小二乗法に基づけば計算できるから正規分布の仮定は必要ない派閥」があることを理解します。
相関係数の定義に従って新しく導入した確率変数で偏相関係数を表します。
多変量正規分布の条件付き分布に関する定理を利用して偏相関係数を求めていきます。
偏相関係数
まずは結論からお伝えします。偏相関係数は以下のように求められます。
「$Z$の影響を除いた$X$」と「$Z$の影響を除いた$Y$」の相関係数を偏相関係数と呼び,以下で表される。
\rho_{x|z, y|z} &= \frac{\rho_{xy} - \rho_{xz}\rho_{yz}}{\sqrt{1 - \rho_{xz}^2}\sqrt{1 - \rho_{yz}^2}}
\end{align}
ただし,$\rho_{xy}$,$\rho_{yz}$,$\rho_{xz}$は通常の相関係数を表す。
偏相関係数を定義にとして捉えるかどうかを悩んだのですが,本書では相関係数の定義を用いて多変量正規分から偏相関係数を導出できるという立場を取ることにしました。
偏相関係数の意味を理解
偏相関係数は「条件付き相関係数」と捉えると一気に理解が進みます。それを今から詳しく説明していきます。前提の立場として,3つの因子$(X, Y, Z)$が与えられたときに,$X$と$Y$を比べたいというモチベーションがあります。「なぜ$2$変数に着目するの」だとか「そもそも何で比較しなきゃいけないの」という疑問は,相関係数を学ぶ立場に立つ以前の議論なので,ここでは対象としません。
3つの因子$(X, Y, Z)$で$X$と$Y$を比べるときに,3つ目の因子$Z$も一緒くたに考えてしまうと,$X$と$Y$に相関がないのに相関があると勘違いしてしまう可能性があります。このような状態を「疑似相関」と呼びます。偏相関係数は疑似相関と密接な関係がある概念です。そこで,まずは疑似相関に対する理解を深めておきましょう。まず,因果関係と相関関係の包含関係についてお伝えしておきます。相関関係は因果関係を包含します。

ゆえに,因果関係があるのであれば必ず相関関係があります。逆に,相関関係があるのに因果関係がない場合もあります。後者のようなケースを「疑似相関」と呼ぶのです。

要するに,疑似相関というのは「因果関係がないのに相関が現れてしまう」状態のことを指しています。偏相関係数は,このような疑似相関を回避するために用いられる概念です。
疑似相関の原因としては,後に述べる共通の因子を持つケースや原因と結果が逆のケースなどがあります。
有名な例を採り上げます。ビールの売り上げと水難事故の発生件数には相関があると言われています。しかし,ビールの売り上げが上がったからといって水難事故が増えると本当に言えるでしょうか。水難事故を起こした人全員が泥酔状態であればその可能性はありますが,泥酔の原因がビールではなく他のお酒の可能性もありますし,なにより水難事故を起こした人全員が泥酔状態であるという仮説は少し乱暴すぎます。逆に,水難事故の発生件数が多くなるからといってビールの売り上げが上がるとは限らないでしょう。水難事故が発生したことをキッカケにビールを買いに行こうと思う人なんて,そうそう居ませんよね。
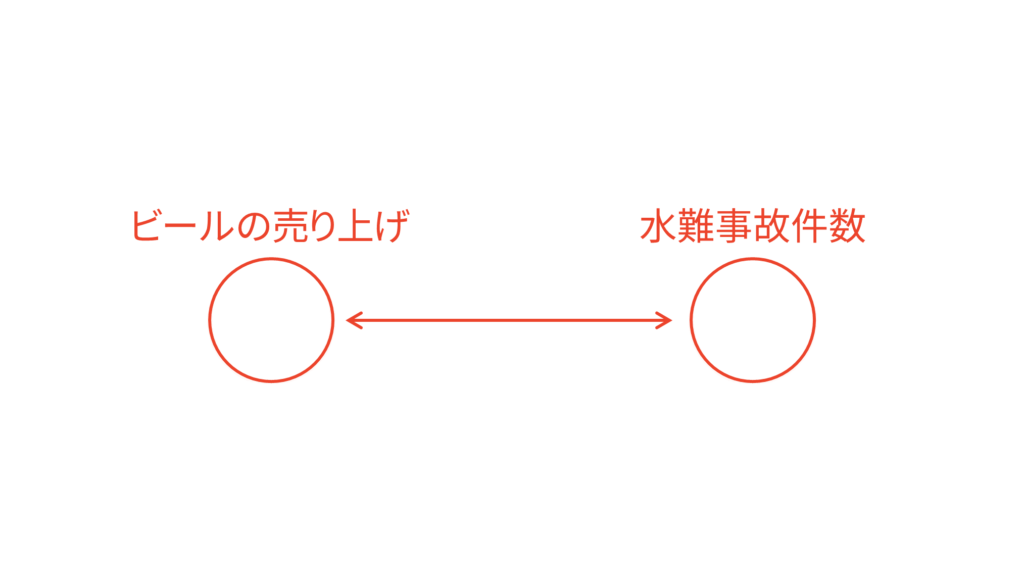
なぜ,ビールの売り上げと水難事故の発生件数には相関があると言われているのでしょうか。恐らく,ビールの売り上げと水難事故の発生件数の裏側には「季節」や「気温」といったような因子が隠れているからだと考えられます。ここでは季節の変化を気温の変化で表すことができると仮定して,「気温」という因子を考えれば十分という立場を取ることにします。気温を考えれば十分季節も考慮できているとする立場ですね。すると,気温が高くなればビールもたくさん売れると考えられますし,気温が高くなればプールや海に行く人が増えて水難事故も発生しやすくなると考えられます。
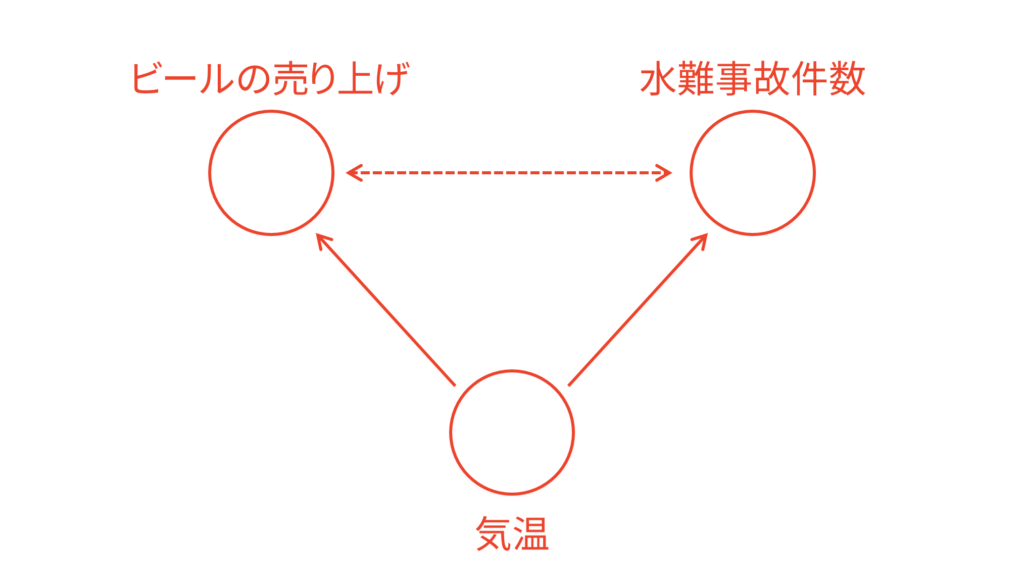
このように,ビールの売り上げと水難事故の発生件数の相関の裏側に「気温」という因子が隠れていることにより,本来関係ないはずの因子に相関関係が確認されてしまったのです。それでは,この気温の影響を取り除いてビールの売り上げと水難事故の発生件数の相関を調査したい場合にはどうすれば良いでしょうか。ここで用いられるのが偏相関係数です。
偏相関係数は,「$Z$の影響を取り除いた$X$」と「$Z$の影響を取り除いた$Y$」の相関を調べることができます。先ほどの例で言うと,「気温の影響を取り除いたビールの売り上げ」と「気温の影響を取り除いた水難事故の発生件数」の相関を調べることができるということです。
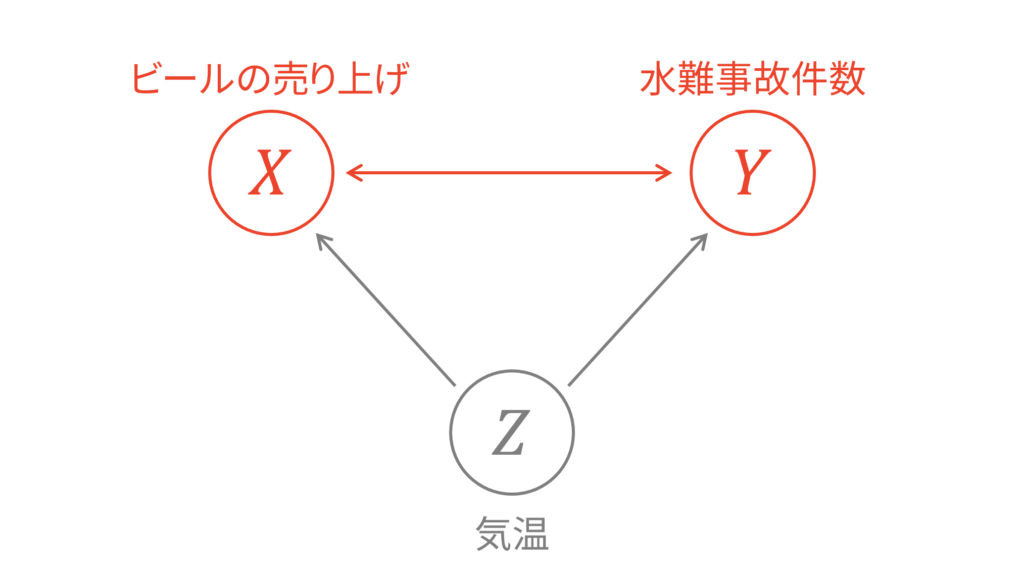
このように確率変数同士の依存関係を図示する手法をグラフィカルモデルと呼びます。機械学習をはじめとして統計的モデリングに広く用いられる手法です。矢印先が矢印元に条件付けされていることを表しています。
偏相関係数はどのように立式すればよいのでしょうか。ここで出てくるのが「条件付き」という概念です。確率変数を条件付けるというのは,複数の値を取り得る確率変数に特定の値(実現値)を仮定することを意味します。もう少し具体的に考えてみます。
$C(X)$を確率変数$X$の個数を表す関数とすると,
C(X|Y=y)
\end{align}
というのは,確率変数$Y$が$y$という値を取るときの確率変数$X$の個数を表しています。繰り返しにはなりますが,「条件付ける」という操作は「他の因子を固定する」という操作に対応します。$C(X|Y=y)$というのは,$Y$の因子を$y$という状態に固定した場合の$X$の個数を表します。これを先ほどの例に当てはめてみましょう。
いま,気温を高い状態に固定するとします。このとき,「気温の影響を取り除いたビールの売り上げ」と「気温の影響を取り除いた水難事故の発生件数」は以下のように表されます。
\text{気温の影響を取り除いたビールの売り上げ} &= C(\text{ビールの売り上げ}|\text{気温}=\text{高い}) \\[0.7em]
\text{気温の影響を取り除いた水難事故の件数} &= C(\text{水難事故の件数}|\text{気温}=\text{高い})
\end{align}
$C(x)$は$X$の個数を表すとしています。ビールの売り上げの場合はビールの個数を表し(もしくは売り上げとして捉えて1円玉の個数としても良いでしょう),水難事故の件数はそのまま件数を表していると考えてOKです。
新しい確率変数の導入
少しずつ文字を導入していきましょう。ビールの売り上げの代わりに$X$,水難事故の発生件数の代わりに$Y$,気温の代わりに$Z$を用います。簡単のため,条件付きの確率変数を新しい確率変数に置き換えましょう。
X^{\ast} &\leftarrow X | Z=z \\[0.7em]
Y^{\ast} &\leftarrow Y | Z=z
\end{align}
このとき,「$Z$の影響を取り除いた$X$」と「$Z$の影響を取り除いた$Y$」の相関は以下のように表されます。
\rho_{x^{\ast}, y^{\ast}} &= \frac{\sigma_{x^{\ast}y^{\ast}}}{\sigma_{x^{\ast}}\sigma_{y^{\ast}}}
\end{align}
ただし,$\sigma_{x^{\ast}}$,$\sigma_{y^{\ast}}$は条件付き標準偏差(条件付き分散の平方根),$\sigma_{x^{\ast}y^
{\ast}}$は条件付き共分散を表します。ちなみに,上の式は通常の相関係数の定義に当てはめただけです。以下では各項を計算していきますが,そのためには相関と回帰の違いを踏まえたうえで,正規分布と相関係数の繋がりを理解する必要があります。
相関との違い
みなさんは相関と回帰の違いを理解できていますか?よく用いられる説明は,相関は双方向的な関係を表し,回帰は一方向的な関係を表しているというものです。
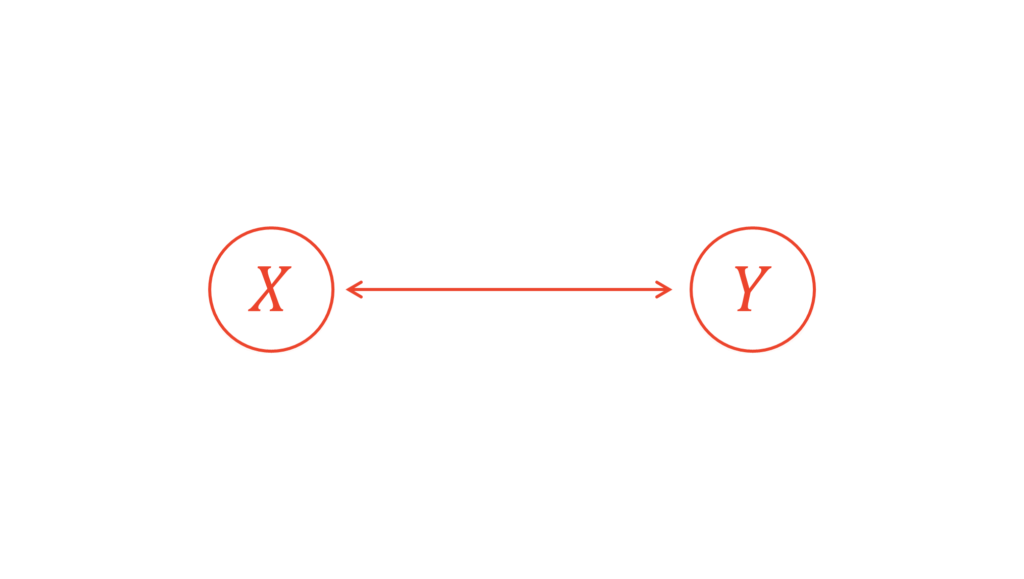
この認識は間違いではありません。ここでは,「双方向的」と「一方向的」に関してある視点を加えたいと思います。先ほどの例を思い出してください。ある因子を特定の状態に固定したかったら,その因子を条件付けてあげればよかったですね。同様に,双方向的な関係を一方向的な関係にしたかったら,確率変数を条件付けてあげればよいのです。
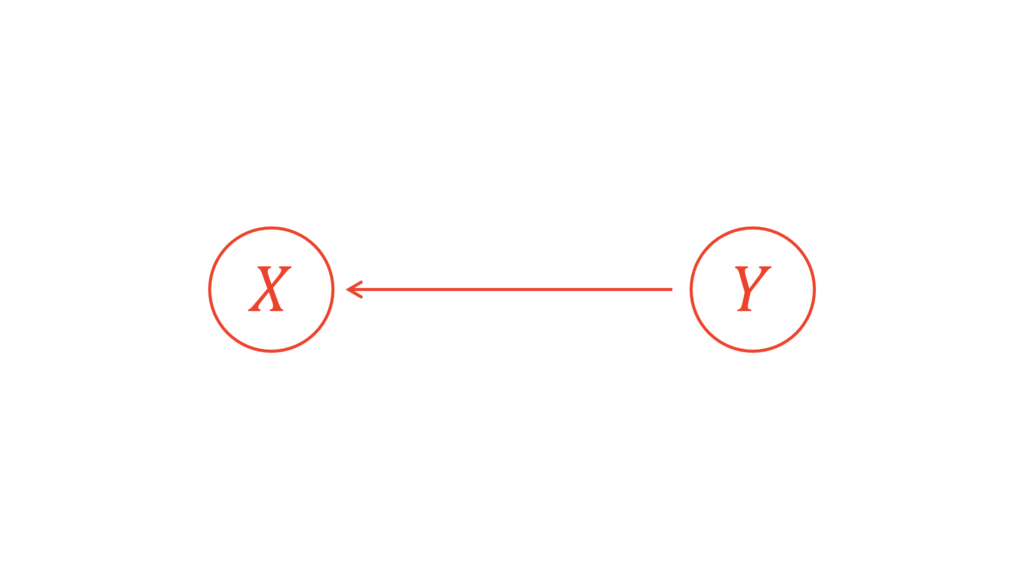
上の図は「$X$は$Y$が与えられたという条件下で得られる」ことを表しています。関数でよく利用する$y=f(x)$は「$X$が与えられたという状況下で得られる$Y$」を表していますから,上の図とは逆であることに注意してください。この記事では,偏相関係数の表記の関係もあって反対にしています。
相関と回帰を「条件付け」という観点でまとめた表を以下に示します。
| 条件付きなし | 条件付きあり | |
| $2$ 変量 | 相関係数 $(X, Y)$ | 回帰 $(X | Y)$ |
| $3$ 変量 | - | 偏相関係数 $(X, Y | Z)$ |
この表を見て分かる通り,偏相関係数というのは「$3$変量の条件付き確率変数」を対象にしています。先ほど示した図をもう一度見てみましょう。

冒頭にお伝えした「偏相関係数が条件付き相関係数と捉えられる」という認識が理解できたでしょうか。
正規分布との繋がり
相関係数は,元々$2$変量正規分布に現れるパラメータとして導入されました。それゆえ,相関係数を計算するデータの母集団は正規分布に従っているべきだという論が存在します。一方で,データの母集団に正規分布を仮定せずに導出できるとする論も存在します。これは,最小二乗法に基づいて相関係数が導出できることが根拠となっています。具体的には,$x\rightarrow y$の回帰係数と$y\rightarrow x$の回帰係数の幾何平均が相関係数になります。
しかし,最小二乗法というのは回帰問題における予測誤差(残差)の二乗に正規分布を仮定したときの最尤推定に相当しますので,最小二乗法に基づいていること自体,データの分布に正規分布を仮定していると言えます。逆に言えば,回帰問題において予測誤差(残差)が正規分布していなければ最小二乗法に基づくフィッティングは適切でないと考えられます。
相関係数に対するスタンスとして「データの分布には正規分布を仮定するべきだ派」と「最小二乗法に基づけば相関係数は計算できるからデータの分布は任意である派」に分かれることが多いですが,これらの背景から,個人的にはデータの分布には正規分布を仮定するべきだと考えています。理由は前述の通り,相関係数が持ち出された経緯が$2$変量正規分布のパラメータであったことに加え,最小二乗法も予測誤差(残差)に正規分布を仮定した最尤推定に相当するからです。
よって,相関係数は$(X, Y)$が$2$変量正規分布に従っていることを出発点とします。同様に,偏相関係数の場合も$(X, Y, Z)$を$3$変量正規分布に従っているものと考えることが出発点です。このような出発点に立てば,条件付き分散や条件付き共分散を正規分布を軸にして計算することができます。
相関係数は「Pearsonの相関係数」とも呼ばれている通り,Pearsonによって相関が発見されたとする説があります。実際には,数学的な観点はBravais,概念的にはGalton,そして両者を結びつけたのがPearsonと言われています [椎名, 2016]。また,正規分布を仮定するという意味で,相関係数や偏相関係数はパラメトリックな手法と呼ばれることがあります。
偏相関係数の式を確認
相関係数の定義を思い出しましょう。
\rho_{xy} &= \frac{\sigma_{xy}}{\sigma_x \sigma_y}
\end{align}
相関係数はこのように求められましたね。この定義式を新しく導入した確率変数で置き換えます。
\rho_{x^{\ast}, y^{\ast}} &= \frac{\sigma_{x^{\ast}y^{\ast}}}{\sigma_{x^{\ast}}\sigma_{y^{\ast}}}
\end{align}
我々が知りたいのはこの式です。何度も言いますが,この式を計算するために以下ではごにょごにょ計算していきます。そのことを忘れないようにしてください。
この式を$(X, Y, Z)$を用いて表すためには,$(X, Y, Z)$に対して何らかの分布を仮定する必要があります。先ほどもお伝えした通り,本記事では$(X, Y, Z)$に$3$次元正規分布を仮定して,それぞれの項である条件付き分散や共分散を計算していきます。
\sigma_{x^{\ast}} &= \sqrt{V[X^{\ast}]} \\[0.7em]
\sigma_{y^{\ast}} &= \sqrt{V[Y^{\ast}]} \\[0.7em]
\sigma_{x^{\ast}y^{\ast}} &= \Cov[X^{\ast}, Y^{\ast}]
\end{align}
ですので,まずは$X$の条件付き分布$f(x|z)$の分散$V[X^{\ast}]$を求めてから,その結果を条件付き分散$V[Y^{\ast}]$に流用し,最後に共分散$\Cov[X^{\ast}, Y^{\ast}]$を求めるという流れにしましょう。
条件付き期待値と分散
さて,$X$の条件付き分布$f(x|z)$の分散$V[X^{\ast}]$を求めていきましょう。定義通りに計算してもよいのですが,ここは既知の定理を組み合わせてスマートに計算していきましょう。まず,多変量正規分布の周辺分布に関する定理より$X$と$Z$はそれぞれ$1$次元正規分布に従っています。一方,$X$と$Z$が独立である保証はないので,同時分布$f(x, z)$は$(X, Z)$を確率変数とする$2$変量正規分布に従います(独立である場合でも$2$次元正規分布と捉えられますが,独立の定義より$1$次元正規分布の積としても表されます)。
言い換えれば,$f(x|z)$を考えるうえでは確率変数$X$と$Z$のみを考えればよく,$Y$は一旦無視しても良いということです。すると,多変量正規分布の条件付き分布に関する定理が利用できます。この定理を利用すると,
V[X^{\ast}] &= \sigma_x^2 - \frac{\sigma_{xz}^2}{\sigma_z^2}
\end{align}
と求められます。この結果を用いて$V[Y^{\ast}]$を求めます。対称性より,$X$と$Y$を置き換えれば良いだけですので,
V[Y^{\ast}] &= \sigma_y^2 - \frac{\sigma_{yz}^2}{\sigma_z^2}
\end{align}
と求められます。あとは,共分散$\Cov[X^{\ast}, Y^{\ast}]$ですね。こちらは定義通りの計算しようとすると,
\Cov[X^{\ast}, Y^{\ast}] &= E[X^{\ast} Y^{\ast}] - E[X^{\ast}] E[Y^{\ast}]
\end{align}
となります。$E[X^{\ast}]$や$E[Y^{\ast}]$はそれぞれ$(X, Z)$,$(Y, Z)$に関する多変量正規分布の条件付き分布に関する定理より求められますが,これらの積を取るのは少し煩雑な計算を要します。さらに,$E[X^{\ast}Y^{\ast}]$を簡単に計算する手段を我々は持っていません。定義通りに計算を進めても良いですが,確率変数の積に関する定義や定理などは少なく,かなり複雑な計算になることは想像に難くありません。
そこで,ここでは多変量正規分布の条件付き分布に関する定理を$3$変量正規分布に対して利用しましょう。以下のように$3$変数に関する行列を$(X, Y)$に関する部分,$(Z)$に関する部分,それ以外の部分に分解します。
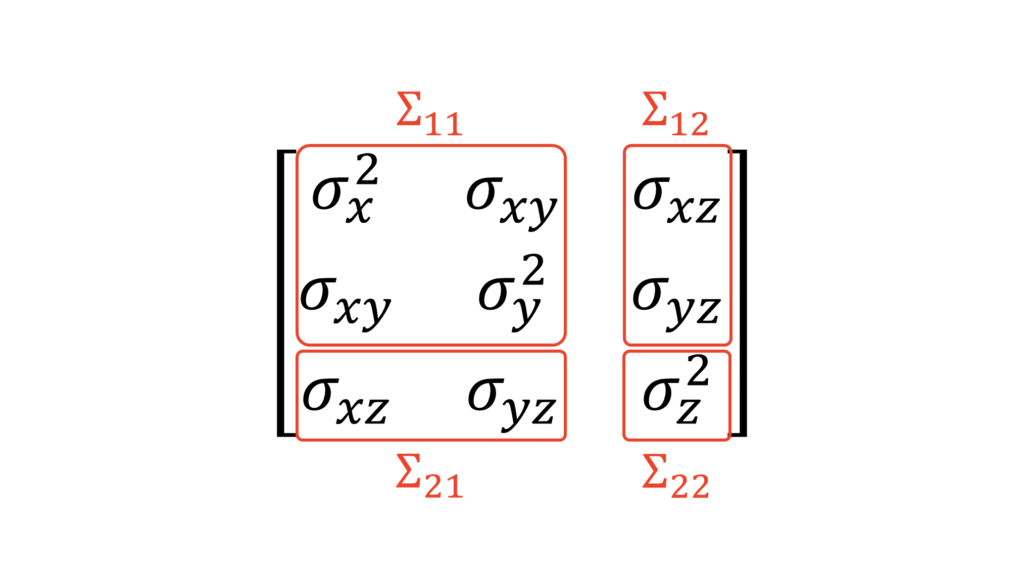
さて, 多変量正規分布の条件付き分布に関する定理に適用していきます。改めて記号を確認すると,
\Sigma_{11} &=
\begin{pmatrix}
\sigma_x^2 & \sigma_{xy} \\
\sigma_{xy} & \sigma_y^2 \\
\end{pmatrix} \\[0.7em]
\Sigma_{12} &=
\begin{pmatrix}
\sigma_{xz} \\
\sigma_{yz} \\
\end{pmatrix} \\[0.7em]
\Sigma_{21} &=
\begin{pmatrix}
\sigma_{xz} & \sigma_{yz} \\
\end{pmatrix} \\[0.7em]
\Sigma_{22} &=
\begin{pmatrix}
\sigma_{z}^2
\end{pmatrix}
\end{align}
となります。したがって,$3$変量正規分布における分散共分散行列$V[X^{\ast}, Y^{\ast}]=V[X, Y|Z]$は以下のようになります。
V[X^{\ast}, Y^{\ast}] &= \Sigma_{11} - \Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21} \\[0.7em]
&=
\begin{pmatrix}
\sigma_x^2 & \sigma_{xy} \\
\sigma_{xy} & \sigma_y^2 \\
\end{pmatrix}
-
\begin{pmatrix}
\sigma_{xz} \\
\sigma_{yz} \\
\end{pmatrix}
\begin{pmatrix}
\sigma_{z}^2
\end{pmatrix}^{-1}
\begin{pmatrix}
\sigma_{xz} & \sigma_{yz} \\
\end{pmatrix} \\[0.7em]
&=
\begin{pmatrix}
\sigma_x^2 & \sigma_{xy} \\
\sigma_{xy} & \sigma_y^2 \\
\end{pmatrix}
-
\frac{1}{\sigma_{z}^2}
\begin{pmatrix}
\sigma_{xz}^2 & \sigma_{xz}\sigma_{yz} \\
\sigma_{xz}\sigma_{yz} & \sigma_{xz}^2 \\
\end{pmatrix} \\[0.7em]
&=
\begin{pmatrix}
\sigma_x^2 - \sigma_{xz}^2/\sigma_{z}^2 & \sigma_{xy} - (\sigma_{xz}\sigma_{yz})/\sigma_{z}^2 \\
\sigma_{xy} - (\sigma_{xz}\sigma_{yz})/\sigma_{z}^2 & \sigma_{y}^2 - 1 \\
\end{pmatrix}
\end{align}
したがって,分散共分散行列の定義より,共分散$\Cov[X^{\ast}, Y^{\ast}]$は以下のようになります。
\Cov[X^{\ast}, Y^{\ast}] &= \sigma_{xy} - \frac{\sigma_{xz}\sigma_{yz}}{\sigma_{z}^2}
\end{align}
以上より,偏相関係数は以下のように計算されます。
\rho_{x^{\ast}, y^{\ast}} &= \frac{\sigma_{x^{\ast}y^{\ast}}}{\sigma_{x^{\ast}}\sigma_{y^{\ast}}} \\[0.7em]
&= \frac{\sigma_{xy} - (\sigma_{xz}\sigma_{yz})/\sigma_{z}^2}{\sigma_x\sqrt{1 - \rho_{xz}^2} \sigma_y\sqrt{1 - \rho_{yz}^2}} \\[0.7em]
&= \frac{\sigma_{xy}/(\sigma_x\sigma_y) - (\sigma_{xz}\sigma_{yz})/(\sigma_x\sigma_y\sigma_{z}^2)}{\sqrt{1 - \rho_{xz}^2} \sqrt{1 - \rho_{yz}^2}} \\[0.7em]
&= \frac{\sigma_{xy}/(\sigma_x\sigma_y)- \sigma_{xz}/(\sigma_x\sigma_z)\cdot (\sigma_{yz}/\sigma_y\sigma_z)}{\sqrt{1 - \rho_{xz}^2} \sqrt{1 - \rho_{yz}^2}} \\[0.7em]
&= \frac{\rho_{xy} - \rho_{xz}\rho_{yz}}{\sqrt{1 - \rho_{xz}^2}\sqrt{1 - \rho_{yz}^2}}
\end{align}
以上で偏相関係数の計算式を導出することができました。ポイントをおさらいしておきましょう。
- 偏相関係数は因果関係がないのに相関関係がある疑似相関を回避するためにある因子に関する影響を排除して計算できる相関係数のこと
- 確率変数を条件付けることはある因子を特定の状態に固定することを意味する
- 条件付いた確率変数を新しく$\ast$を付けて置き換えることで分かりやすい議論を展開することが可能
- 相関係数を計算するうえでデータの分布に正規分布を仮定する派閥と仮定しない派閥が存在する
- 本記事ではデータの分布に正規分布を仮定する立場を取る
- 条件付き分散を求めるためには$2$変量正規分布の条件付き分布に関する定理を利用する
- 条件付き共分散を求めるためには$3$変量正規分布の条件付き分布に関する定理を利用する
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント