統計検定1級の過去問解答解説を行います。目次は以下をご覧ください。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
問題
統計検定1級の過去問からの出題になります。統計検定の問題の著作権は日本統計学会に帰属していますので,本稿にて記載することはできません。「演習問題を俯瞰する」で詳しく紹介している公式の過去問題集をご購入いただきますようお願い致します。
解答
パレート分布の最尤推定と期待値・分散の性質に関する出題でした。
(1)
f(x) &=
\begin{cases}
\displaystyle
\frac{1}{\gamma}x^{-1/\gamma-1}&(x>1)\\[0.7em]
0&(x\leq 1)
\end{cases}
\end{align}
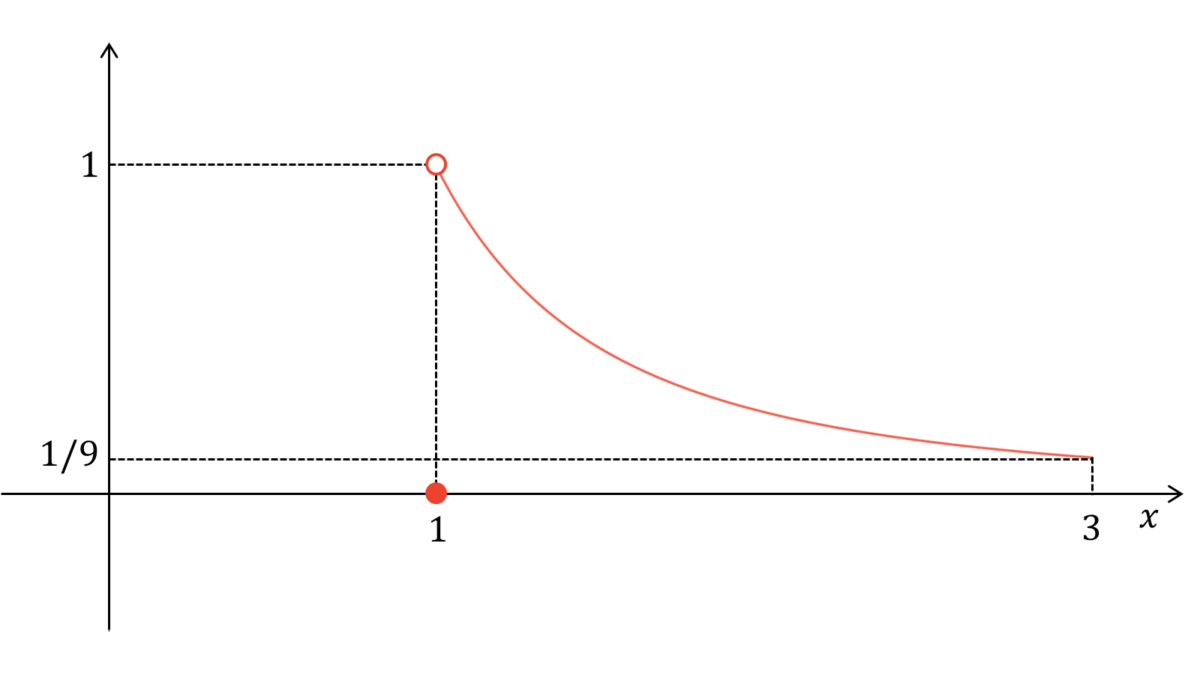
累積分布関数と確率密度関数の関係より,$x>1$のとき
f(x) &= \frac{d}{dx}\left(1-x^{-1/\gamma}\right) = \frac{1}{\gamma}x^{-1/\gamma-1}
\end{align}
が成りたちます。同様に,$x\leq 1$のとき$f(x){=}0$が成り立ちます。したがって,$\gamma=1$のときは,
f(x) &=
\begin{cases}
x^{-2}&(x>1)\\[0.7em]
0&(x\leq 1)
\end{cases}
\end{align}
となり,$1\leq x\leq 3$の範囲で$f(x)$の概形は上の解答のようになります。
(2)
E[X] &=
\begin{cases}
\displaystyle
\frac{1}{1-\gamma}&(0<\gamma<1)\\[0.7em]
\text{発散}&(1\leq\gamma)
\end{cases}\\[0.7em]
V[X] &=
\begin{cases}
\displaystyle
\frac{\gamma^{2}}{(1-2\gamma)(1-\gamma)^{2}}&\displaystyle\left(0<\gamma<\frac{1}{2}\right)\\[0.7em]
\displaystyle
\text{発散}&\displaystyle\left(\frac{1}{2}\leq\gamma\right)
\end{cases}
\end{align}
期待値の定義より,$x\leq 1$のとき$f(x)=0$となることに注意すると,
E[X] &= \int_{1}^{\infty}x\cdot \frac{1}{\gamma}x^{-1/\gamma-1}dx
= \frac{1}{\gamma}\int_{1}^{\infty}x^{-1/\gamma}dx
\end{align}
となります。ここで,$\gamma=1$のときは,
E[X] &= \int_{1}^{\infty}x^{-1/\gamma}dx = \left[\log x\right]_{1}^{\infty}
\end{align}
となり,$E[X]$は発散してしまいます。そこで,$\gamma\neq 1$のとき,
E[X] &= \frac{1}{\gamma}\left[\frac{\gamma}{\gamma-1}x^{(\gamma-1)/\gamma}\right]_{1}^{\infty}
\end{align}
となりますが,$x$の指数部分に着目すると,$E[X]$の収束条件は$0<\gamma<1$となります。このとき,
E[X] &= \frac{1}{1-\gamma}
\end{align}
が得られます。同様に,$E[X^{2}]$は
E[X^{2}]
&= \frac{1}{\gamma}\int_{1}^{\infty}x^{-1/\gamma+1}dx
= \frac{1}{\gamma}\left[\frac{\gamma}{2\gamma-1}x^{(2\gamma-1)/\gamma}\right]_{1}^{\infty}
= \frac{1}{1-2\gamma}
\end{align}
となりますが,$x$の指数部分に着目すると,$E[X]$の収束条件は$0{<}\gamma{<}1/2$となります。したがって,$0{<}\gamma{<}1/2$のとき,分散の定義より
V[X] &= E[X^{2}]-E[X]^{2}\\[0.7em]
&= \frac{1}{1-2\gamma} - \left(\frac{1}{1-\gamma}\right)^{2}\\[0.7em]
&= \frac{\gamma^{2}}{(1-2\gamma)(1-\gamma)^{2}}
\end{align}
が得られます。
(3)
\hat{\gamma} &= \frac{1}{n}\sum_{i=1}^{n}\log X_{i}\label{3-1}
\end{align}
$X=(X_{1},\ldots,X_{n})$とおくと,$X_{1},\ldots,X_{n}$がそれぞれ互いに独立であることから,$X$の同時確率密度関数$g$は
g(x) &= \prod_{i=1}^{n}f(x_{i})
=
\begin{cases}
\displaystyle
\frac{1}{\gamma^{n}}\prod_{i=1}^{n}x_{i}^{-1/\gamma-1}&(x>1)\\[0.7em]
0&(x\leq 1)
\end{cases}
\end{align}
となります。したがって,$x>1$のとき,対数尤度$\log L(\gamma)$は
\log L(\gamma) &=
-n\log\gamma-\left(\frac{1}{\gamma}+1\right)\sum_{i=1}^{n}\log x_{i}
\end{align}
と表されます。両辺を$\gamma$で微分して$0$とおくと,
\frac{\partial\gamma}{\partial}\log L(\gamma)
&= -\frac{n}{\gamma}+\frac{1}{\gamma^{2}}\sum_{i=1}^{n}\log x_{i} = 0
\end{align}
となります。これを$\gamma$について解くと,最尤解は式($\ref{3-1}$)のようになります。
(4)
T&\sim\Exp(1)
\end{align}
$T=\log X/\gamma$を変形すると$X=e^{\gamma T}$であり,$dx/dt{=}\gamma e^{\gamma t}$より,$T$の従う分布の確率密度関数を$g(t)$とおくと,$x>1$のとき,すなわち$t>0$のとき,
g(t) &= f(e^{\gamma t})\frac{dx}{dt}
= \frac{1}{\gamma}\cdot e^{\gamma t(-1/\gamma-1)}\cdot\gamma e^{\gamma t}
= e^{-t}
\end{align}
が得られます。これは,パラメータ$1$の指数分布$\Exp(1)$の確率密度関数となりますので,$T\sim\Exp(1)$となります。指数分布に関しては,以下をご参照ください。
(5)
E[\hat{\gamma}] &= \gamma\\[0.7em]
V[\hat{\gamma}] &= \frac{\gamma^{2}}{n}
\end{align}
指数分布$\Exp(\lambda)$に従う確立変数$X$の期待値と分散は,$E[X]=1/\lambda$,$V[X]=1/\lambda^{2}$となることを利用すると,$E[T]{=}V[T]{=}1$となります。
確率変数の線形結合と期待値の性質を利用すると,$\hat{\gamma}$の期待値は,
E[\hat{\gamma}] &=
E\left[\frac{1}{n}\sum_{i=1}^{n}\log X_{i}\right]
= \frac{1}{n}\sum_{i=1}^{n}E\left[\gamma T\right]
= \frac{\gamma }{n}\sum_{i=1}^{n}E\left[T\right]
= \frac{\gamma}{n}\sum_{i=1}^{n}1
= \gamma
\end{align}
と求められます。同様に,$X_{1},\ldots,X_{n}$が独立であることに注意して確率変数の線形結合と分散の性質を利用すると,$\hat{\gamma}$の分散は,
V[\hat{\gamma}] &=
V\left[\frac{1}{n}\sum_{i=1}^{n}\log X_{i}\right]
= \frac{1}{n^{2}}\sum_{i=1}^{n}V\left[\gamma T\right]
= \frac{\gamma^{2}}{n^{2}}\sum_{i=1}^{n}V\left[T\right]
= \frac{\gamma^{2}}{n^{2}}\sum_{i=1}^{n}1
= \frac{\gamma^{2}}{n}
\end{align}
と求められます。


コメント