統計検定1級の過去問解答解説を行います。目次は以下をご覧ください。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
問題
統計検定1級の過去問からの出題になります。統計検定の問題の著作権は日本統計学会に帰属していますので,本稿にて記載することはできません。「演習問題を俯瞰する」で詳しく紹介している公式の過去問題集をご購入いただきますようお願い致します。
解答
コーシー分布と最強力検定に関する出題です。
(1)
\alpha &\approx 0.148
\end{align}
第一種の過誤確率は真である帰無仮説が棄却される確率ですので,
\alpha &= P(1<X<3|\theta=0)
{=} \int_{1}^{3}\frac{1}{\pi(1+x^{2})}dx
{=} \frac{1}{\pi}\left(\tan^{-1}3-\frac{\pi}{4}\right)
{=} \frac{1.2490}{3.1416}-\frac{1}{4}
\approx 0.148
\end{align}
と求められます。
(2)
1-\beta &\approx 0.352
\end{align}
第二種の過誤確率は偽である帰無仮説が棄却されない確率であるため,
1-\beta &= P(1{<}X{<}3|\theta{=}1)
{=} \int_{1}^{3}\frac{1}{\pi\left\{1+(x-1)^{2}\right\}}dx
{=} \frac{1}{\pi}\left(\tan^{-1}2-0\right)
{=} \frac{1.107}{3.1416}
\approx 0.352
\end{align}
と求められます。
(3)
$\lambda(1)=\lambda(3)=2$であり,グラフは下記のようになる。
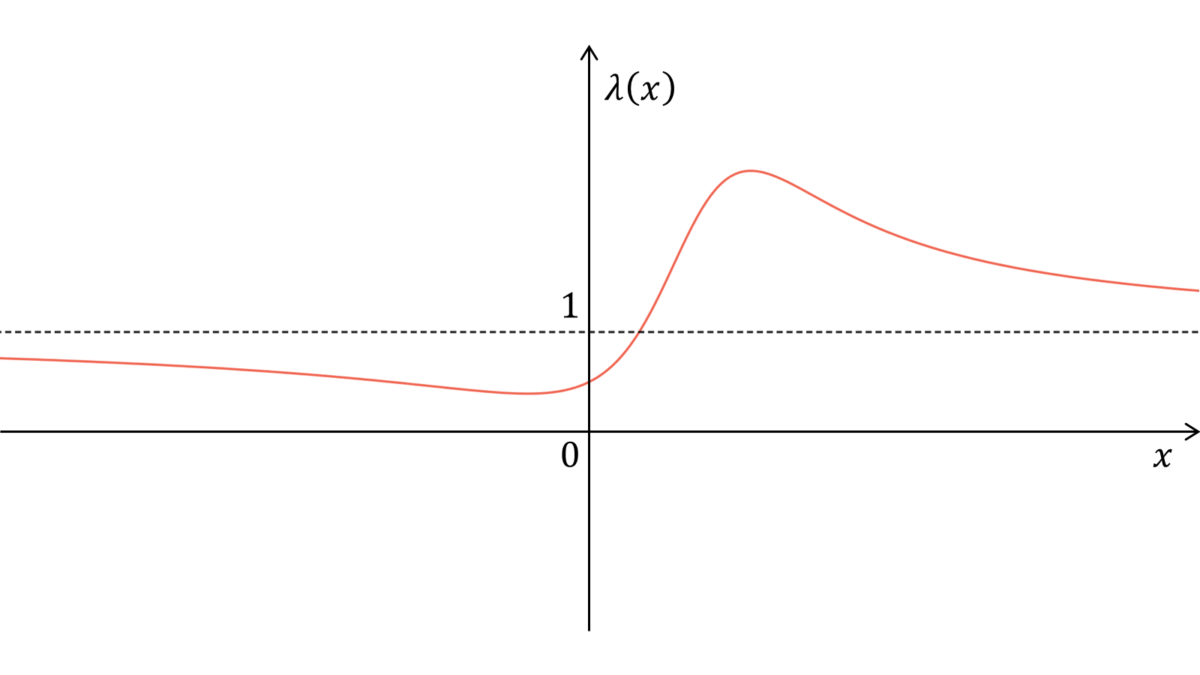
まずは尤度比$\lambda(x)$を計算します。
\lambda(x) &= \frac{f_{1}(x)}{f_{0}(x)}
= \frac{\pi\left\{1+(x-0)^{2}\right\}}{\pi\left\{1+(x-1)^{2}\right\}}
= \frac{1+x^{2}}{1+(x-1)^{2}}
\end{align}
したがって,
\lambda(1) &= \lambda(3) = 2
\end{align}
と計算できます。$\lambda(x)$の外形を描くため,導関数が$0$になる$x$と$x\rarr\pm\infty$の極限を調べましょう。まず,$\lambda(x)$の導関数を$0$とおくと,
\lambda^{\prime}(x) &= \frac{2x\left\{1+(x-1)^{2}\right\}-(1+x^{2})2(x-1)}{\left\{1+(x-1)^{2}\right\}^{2}}
= \frac{-2(x^{2}-x-1)}{\left\{1+(x-1)^{2}\right\}^{2}}
= 0
\end{align}
となります。したがって,$\lambda^{\prime}(x)=0$を満たす$x$のうち小さい方を$a$,大きい方を$b$とおくと,
a &= \frac{1-\sqrt{5}}{2},\quad b = \frac{1+\sqrt{5}}{2}
\end{align}
となります。一方,$x\rarr\pm\infty$の極限は,
\lim_{x\rarr\pm\infty}\lambda(x) &= \lim_{x\rarr\pm\infty}\frac{1/x^{2}+1}{1/x^{2}+(1-1/x)^{2}} = 1
\end{align}
となります。したがって,増減表は以下のようになります。
| $x$ | $-\infty$ | $\cdots$ | $a$ | $\cdots$ | $1$ | $\cdots$ | $b$ | $\cdots$ | $3$ | $\cdots$ | $\infty$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| $\lambda(x)$ | $1$ | $\cdots$ | $\lambda(a)$ | $\cdots$ | $2$ | $\cdots$ | $\lambda(b)$ | $\cdots$ | $2$ | $\cdots$ | $1$ |
$\lambda(a)<1$に注意すると,グラフは上の解答のようになります。
(4)
ネイマン・ピアソンの基本定理より,棄却域$R$は尤度比$\lambda(x)>2$を満たす領域であるため,与えられた検定は小問(1)で求められたサイズにおいて最強力検定となる。
ネイマン・ピアソンの基本定理により,尤度比を調べることで最強力検定かどうかを判定できます。


コメント