【徹底解説】NMFをはじめからていねいに

本記事は機械学習の徹底解説シリーズに含まれます。

初学者の分かりやすさを優先するため，多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。

はじめに

非負値行列因子分解（NMF：Nonnegative matrix factorization）は，非負値のデータを要素にもつ行列を，頻出パターン行列とその係数行列に分解する多変量解析の手法です [1]。Leeらによって効率的な更新アルゴリズム [2] が発見されて以来，文書データ [3] や音源分離 [4] など様々な分野で応用されています。NMFの利点は，以下の三点に集約されます。

NMFは行列が非負値であるという制限から数値計算で減算されることがないため，正負の値をとり得る行列を扱う主成分分析や特異値分解とは異なる解析結果が得られます。実際，Leeらによって導かれた反復的な更新式は，乗算近似であるため各要素の非負値性を保持するアルゴリズムとなっています。このような性質のことをスパース性，または低ランク性とよびます。また，NMFの更新式では乖離度とよばれる様々な近似の指標を用います。乖離度には任意の関数を設定することが可能ですが，特定の関数を設定することにより，確率的生成モデルによる理論的な裏付けが可能になります。

問題設定

NMFの目的は，ある非負値行列を二つの非負値行列の積で近似することです。

ただし，$\mY\in\bbR^{L\times N}$を観測行列，$\mH\in\bbR^{L\times M}$を基底行列，$\mU\in\bbR^{M\times N}$を係数行列とします。$M<\min(L,N)$のときは，NMFは観測行列を少数の基底で近似します。ここで，以降の議論を簡潔に行うため，各行列を構成するベクトルを定義します。

これらのベクトルを用いると，行列積の定義より式($\ref{問題設定}$)は以下のように表されます。

繰り返しますが，我々の目的は観測行列$\mY$を$\mH$と$\mU$の積で近似することです。近似を行うためには，$\mY$と$\mH\mU$がどれだけ数学的に離れているかを評価する必要があります。この指標は乖離度とよばれ，NMFでは以下の三種類が主に利用されます。なお，乖離度は数学的な距離の公理を満たすとは限りません。

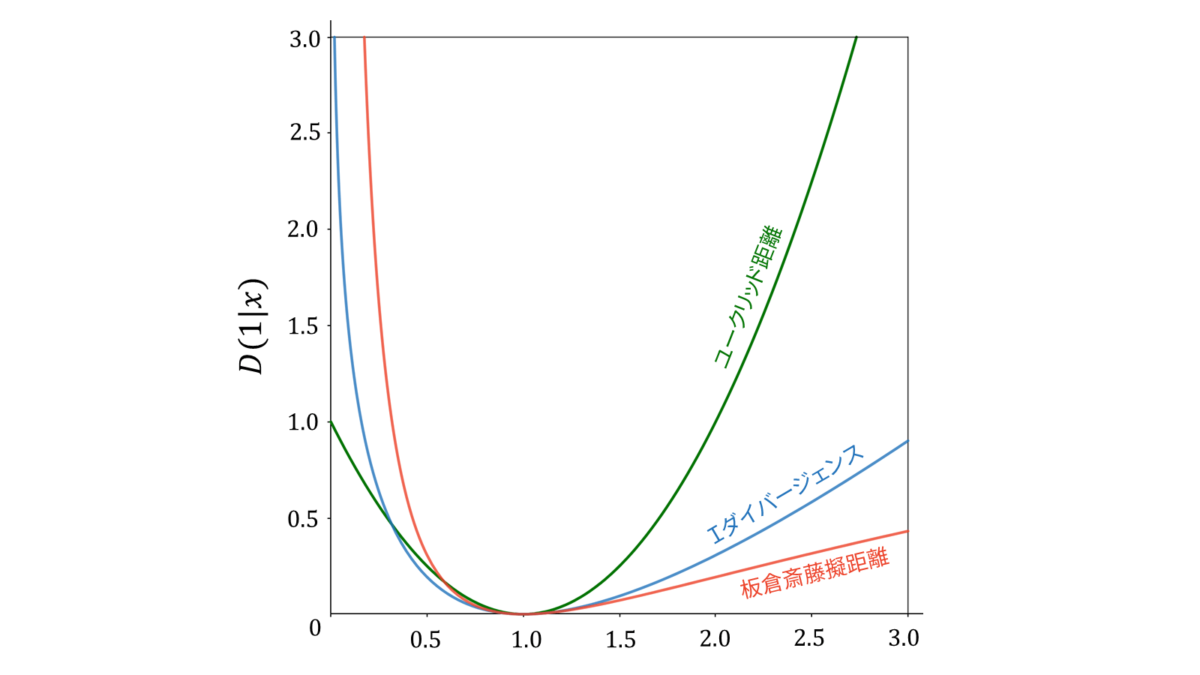
いずれの乖離度も，$x=y$のときに最小値$0$をとり，$x$と$y$の値が離れるほど増加する関数です。ユークリッド距離は$y$を中心に左右対称であるのに対し，$\I$ダイバージェンスと板倉斎藤擬距離は非対称であり，値が大きくなりすぎることに対しては許容しますが，値が小さくなりすぎることには敏感です。加えて，$\I$ダイバージェンスは$x$が$y$を上回るとき，板倉斎藤擬距離は$x$が$y$を下回るときに大きなペナルティを課します。また，式($\ref{板倉斎藤擬距離}$)から分かる通り，板倉斎藤擬距離は$x$と$y$の比のみで表されているため，$x$と$y$のスケールに依存しません。

音源分離では，板倉斎藤擬距離基準のNMFはスペクトルピークの一致度を重要視することや，音響信号の低域と高域を同等の重要度で扱うことを可能にし，$\I$ダイバージェンスを乖離度に用いるよりも経験的に高い性能を発揮することが知られています [5], [6], [7]。また，$\I$ダイバージェンスは一般化$\KL$ダイバージェンスと呼ばれることもあります。

乖離度の選択には，背後に仮定された生成モデルについても考慮する必要があります。ユークリッド二乗距離，$\I$ダイバージェンス，板倉斎藤擬距離を乖離度とするNMFは，観測行列の要素$y_{l,n}$が$x_{l,n}$を平均とした正規分布，ポアソン分布，指数分布に従って独立に生成されたと仮定した場合の$\mH, \mU$の最尤推定問題と等価になります。詳しくは後述します。

以上をまとめます。乖離度を$D(\mY|\mH\mU)$とおくと，NMFは以下の最適化問題として定式化されます。

ただし，subject toは「〇〇という制約の下で」を意味し，$\forall$は「全ての〇〇」を意味します。すなわち，NMFでは行列$\mH$と$\mU$の全ての要素が非負であるという条件の下で，$D(\mY|\mH\mU)$を最小にする非負値行列$\mH,\mU$を求めるという問題を解きます。

補足

上で紹介した三つの乖離度に加え，理論的な議論を行うため以下の二つの乖離度が用いられることもあります。$\beta$ダイバージェンス，Bregmanダイバージェンスを乖離度とするNMFは，それぞれ観測行列の要素$y_{l,n}$が$x_{l,n}$を平均としたTweedie分布，指数分布族に従って独立に生成されたと仮定した場合の$\mH, \mU$の最尤推定問題と等価になります。

$\beta$ダイバージェンスは$\beta\neq 0,1$で定義され，$\beta\rarr 0$のときは板倉斎藤擬距離，$\beta\rarr 1$のときは$\I$ダイバージェンス，$\beta=2$のときはユークリッド距離に相当します。ゆえに，$\beta$ダイバージェンスは板倉斎藤擬距離，$\I$ダイバージェンス，ユークリッド距離の一般化といえます。さらに，Bregmanダイバージェンスは，$\varphi:~\bbR\rarr\bbR$を任意の微分可能な関数として定義されます。$\varphi$に適当な関数を仮定することで，Bregmanダイバージェンスは$\beta$ダイバージェンスとなりますので，Bregmanダイバージェンスは$\beta$ダイバージェンスの一般化といえます。

更新式の導出

我々の目的は，$D(\mY|\mH\mU)$を最小化する$\mH$と$\mU$を見つけることです。この最適化問題は解析的に解くことが難しいため，NMFでは補助関数法を用います。

補助関数である目的関数の上限を探すために，以下のイェンセン（Jensen）の不等式と接線の不等式がよく用いられます。

以下では，これらの不等式と補助関数法を用いて，乖離度にユークリッド距離，$\I$ダイバージェンス，板倉斎藤擬距離を用いた場合のNMFの更新式を導出していきます。

ユークリッド距離

最初に結論を述べます。

早速更新式の導出を始めます。簡単のため，行列表記でなく要素を書き下す形で計算します。

この式を最小にする$h_{l,m}$と$u_{m,n}$を求めればよいのですが，第二項目が合成関数の形になっており微分してもシグマが残ってしまうため，解析的に解くことができません。そこで，上で述べた補助関数法を用いて反復的に近似解を求めるアプローチをとりたいと思います。

補助関数法を用いるために，$D_{\EU}$の上限を求めましょう。上限を求めるためには，第二項目が$f(x)=x^{2}$の形になっていることに注目して，上で述べたイェンセンの不等式を利用します。そのために，

を満たす補助変数$\lambda_{l,m,n}$を無理やり導入します。

ただし，二階微分が正であるならば狭義凸であること，すなわち$f(x)=x^{2}$に対し$f^{\prime\prime}(x)=2>0$であるから$f(x)=x^{2}$は狭義凸であることを利用しました。また，イェンセンの不等式の等号成立条件より，等号は

のとき成り立ちます。式($\ref{ユークリッド_等号成立_タネ}$)と$\lambda_{l,m,n}$の制約条件($\ref{lambda_制約条件}$)から等号を成立させる$\lambda_{l,m,n}$を求めましょう。まず，式($\ref{ユークリッド_等号成立}$)を$\lambda_{l,1,n}$についてまとめると，以下のようになります。

これを$\lambda_{l,m,n}$の制約条件($\ref{lambda_制約条件}$)に代入します。

すなわち，以下が得られます。

$m=2,\ldots,M$に対して同じ手続きを施すことにより，等号成立条件は以下のようになります。

ここで，表記を簡潔にするために$\lambda_{l,m,n}$の行列表記を導入します。

式($\ref{ユークリッド_等号成立}$)により式($\ref{ユークリッド_上限}$)が最小化されますので，式($\ref{ユークリッド_上限}$)の上限は補助関数，$\Lambda$は補助変数の要件を満たしています。改めて式($\ref{ユークリッド_上限}$)の上限を$G_{\EU}(\mH,\mU,\mLambda)$とおくと，

が成り立ちます。あとは補助関数法に従い，$G_{\EU}$を最小にする$\mH$と$\mU$を求めるだけです。$G_{\EU}$をよく観察すると，$h_{l,m}$と$u_{m,n}$に対して二次関数の形をしていますので，$h_{l,m}$と$u_{m,n}$それぞれで偏微分した導関数が$0$となる値が$G_{\EU}$を最小にする値となります。

狭義凸関数は，極小値が存在するならば最小値だけであるという性質をもちます。したがって，狭義凸関数$f(x)=x^{2}$に対して$f^{\prime}(\hatx)=0$を満たす$\hatx$が存在するのであれば，$f(\hatx)$は最小値となることが保証されます。

しかし，$h_{l,m}$と$u_{m,n}$は非負であるという制約がありますので，もし導関数を$0$にする値が負となる場合には，$0$が$G_{\EU}$を最小化する値になります。すなわち，$G_{\EU}$の導関数を$0$にする$h_{l,m}$と$u_{m,n}$をそれぞれ$\hath_{l,m},\hatu_{m,n}$とおくと，補助関数法に基づくユークリッド距離を乖離度としたNMFの更新式は以下で求められます。

まずは，$G_{\EU}$の$\mH$に関する導関数が$0$になるという条件を考えます。

これを整理すると，以下が得られます。

次に，$G_{\EU}$の$\mU$に関する導関数が$0$になるという条件を考えます。

これを整理すると，以下が得られます。

さて，式($\ref{ユークリッド_等号成立}$)，式($\ref{ユークリッド_h}$)，式($\ref{ユークリッド_u}$)を式($\ref{ユークリッド_max_h}$)，式($\ref{ユークリッド_max_u}$)に代入すればよいのですが，式($\ref{ユークリッド_等号成立}$)，式($\ref{ユークリッド_h}$)，式($\ref{ユークリッド_u}$)を観察してみると，$\mY$が非負値かつ$\mH,\mU$の初期値に非負値を与えた場合には，これらの式は必ず非負の値をとることが分かります。したがって，式($\ref{ユークリッド_max_h}$)，式($\ref{ユークリッド_max_u}$)は不要になり，式($\ref{ユークリッド_等号成立}$)，式($\ref{ユークリッド_h}$)，式($\ref{ユークリッド_u}$)を更新式として採用すればよいことが分かります。

$\mLambda$はこちら側の都合で勝手に導入した補助変数ですので，最後の仕上げとして式($\ref{ユークリッド_等号成立}$)は式($\ref{ユークリッド_h}$)，式($\ref{ユークリッド_u}$)に代入して$\lambda_{l,m,n}$を消去した形にしてあげます。以上より，冒頭の更新式が示されました。

Iダイバージェンス

最初に結論を述べます。

更新式の導出方法は，ユークリッド距離の場合と同様です。

この式を最小にする$h_{l,m}$と$u_{m,n}$を求めればよいのですが，第一項目がlog-sumの形になっており解析的に解くことができません。そこで，上で述べた補助関数法を用いて反復的に近似解を求めるアプローチをとりたいと思います。

補助関数法を用いるために，$D_{\I}$の上限を求めましょう。上限を求めるためには，第一項目が$f(x)=-\log x$になっていることに注目して，上で述べたイェンセンの不等式を利用します。そのために，ユークリッド距離基準の更新式導出でも利用した補助変数$\lambda_{l,m,n}$を無理やり導入します。

ただし，二階微分が正であるならば狭義凸であること，すなわち$f(x){=}{-}\log x$に対し$f^{\prime\prime}(x)=1/x^{2}>0$であるから$f(x){=}{-}\log x$は狭義凸であることを利用しました。また，イェンセンの不等式の等号成立条件より，等号は

のとき成り立ちます。これは，ユークリッド距離の等号成立条件($\ref{ユークリッド_等号成立_タネ}$)と全く同じ形をしていますので，等号成立条件は以下のようになります。

式($\ref{I_等号成立}$)により式($\ref{I_上限}$)が最小化されますので，式($\ref{I_上限}$)の上限は補助関数，$\Lambda$は補助変数の要件を満たしています。改めて式($\ref{I_上限}$)の上限を$G_{\I}(\mH,\mU,\mLambda)$とおくと，

が成り立ちます。あとは補助関数法に従い，$G_{\I}$を最小にする$\mH$と$\mU$を求めるだけです。$G_{\I}$をよく観察すると，$h_{l,m}$と$u_{m,n}$に対して$-\log x + x$の形をしていますので，$h_{l,m}$と$u_{m,n}$それぞれで偏微分した導関数が$0$となる値が$G_{\I}$を最小にする値となります。

上で説明した通り，狭義凸関数には極小値が存在するならば最小値だけであるという性質があります。したがって，狭義凸関数$f(x)=-\log x + x$に対して$f^{\prime}(\hatx)=0$を満たす$\hatx$が存在するのであれば，$f(\hatx)$は最小値となることが保証されます。さらに，$\log x$の定義域は$x>0$であることから，ユークリッド距離基準の更新式の導出過程とは異なり，$h_{l,m}$と$u_{m,n}$は非負であるという制約は既に課せられています。

まずは，$G_{\I}$の$\mH$に関する導関数が$0$になるという条件を考えます。

これを整理すると，以下が得られます。

次に，$G_{\I}$の$\mU$に関する導関数が$0$になるという条件を考えます。

これを整理すると，以下が得られます。

$\mLambda$はこちら側の都合で勝手に導入した補助変数ですので，最後の仕上げとして式($\ref{I_等号成立}$)は式($\ref{I_h}$)，式($\ref{I_u}$)に代入して$\lambda_{l,m,n}$を消去した形にしてあげます。以上より，冒頭の更新式が示されました。

板倉斎藤擬距離

最初に結論を述べます。

更新式の導出方法は，ユークリッド距離・$\I$ダイバージェンスに基づく更新式はLeeらによって導かれましたが，板倉斎藤擬距離に基づく更新式はFevotteらによって導かれました。

実はFevotteらよりも早く、亀岡らによりNMFとは別文脈で補助関数法を用いた板倉斎藤擬距離に基づく最適化手法が提案されています。

とはいえ，更新式の導出方法の大枠はユークリッド距離の場合と同様です。

この式を最小にする$h_{l,m}$と$u_{m,n}$を求めればよいのですが，第一項目・第二項目のいずれも合成関数の形になっており微分してもシグマが残ってしまうため，解析的に解くことができません。そこで，上で述べた補助関数法を用いて反復的に近似解を求めるアプローチをとりたいと思います。

補助関数法を用いるために，$D_{\IS}$の上限を求めましょう。ただし，今回はユークリッド距離・$\I$ダイバージェンスとは異なり，式($\ref{上限_タネ}$)の第一項目と第二項目に$h_{l,m}$と$u_{m,n}$が使われていますので，補助変数と補助関数の要件を満たす上限を求めるためにはそれぞれ関する上限を求める必要があります。そこで，まずは第一項目に関する上限を求めましょう。第一項目が$f(x)=1/x$の形になっていることに注目して，上で述べたイェンセンの不等式を利用します。そのために，ユークリッド距離基準の更新式導出でも利用した補助変数$\lambda_{l,m,n}$を無理やり導入します。

ただし，二階微分が正であるならば狭義凸であること，すなわち$x{>}0$の$f(x)=1/x$に対し$f^{\prime\prime}(x){=}2/x^{3}{>}0$より$f(x){=}1/x$は狭義凸であることを利用しました。また，イェンセンの不等式の等号成立条件より，等号は

のとき成り立ちます。これは，ユークリッド距離の等号成立条件($\ref{ユークリッド_等号成立_タネ}$)と全く同じ形をしていますので，等号成立条件は以下のようになります。

続いて，式($\ref{上限_タネ}$)の第二項目に対して上限を求めます。$f(x){=}\log x$は$f^{\prime\prime}(x){=}{-}x^{-2}{<}0$より，$f(x){=}\log x$は狭義凹となりますので，イェンセンの不等式ではなく接線の不等式を利用します。

ただし，$\sum_{m=1}^{M}h_{l,m}u_{m,n}=x_{l,n}$とおきました。接線の不等式の等号成立条件より，等号は

のとき成り立ちます。ここで，表記を簡潔にするために$\alpha_{l,n}$の行列表記を導入します。

式($\ref{IS_等号成立1}$)と式($\ref{IS_等号成立2}$)により式($\ref{IS_上限}$)が最小化されますので，式($\ref{IS_上限}$)の上限は補助関数，$\Lambda$と$\valpha$は補助変数の要件を満たしています。改めて式($\ref{IS_上限}$)の上限を$G_{\IS}(\mH,\mU,\mLambda,\valpha)$とおくと，

が成り立ちます。あとは補助関数法に従い，$G_{\IS}$を最小にする$\mH$と$\mU$を求めるだけです。$G_{\IS}$をよく観察すると，$h_{l,m}$と$u_{m,n}$に対して$x^{-1}{+}\log x$の形をしていますが，これは狭義凸でも狭義凹でもありません。しかし，以下のようにグラフを描いてみると，$h_{l,m}$と$u_{m,n}$それぞれで偏微分した導関数が$0$となる値が$G_{\EU}$を最小にする値となることが分かります。

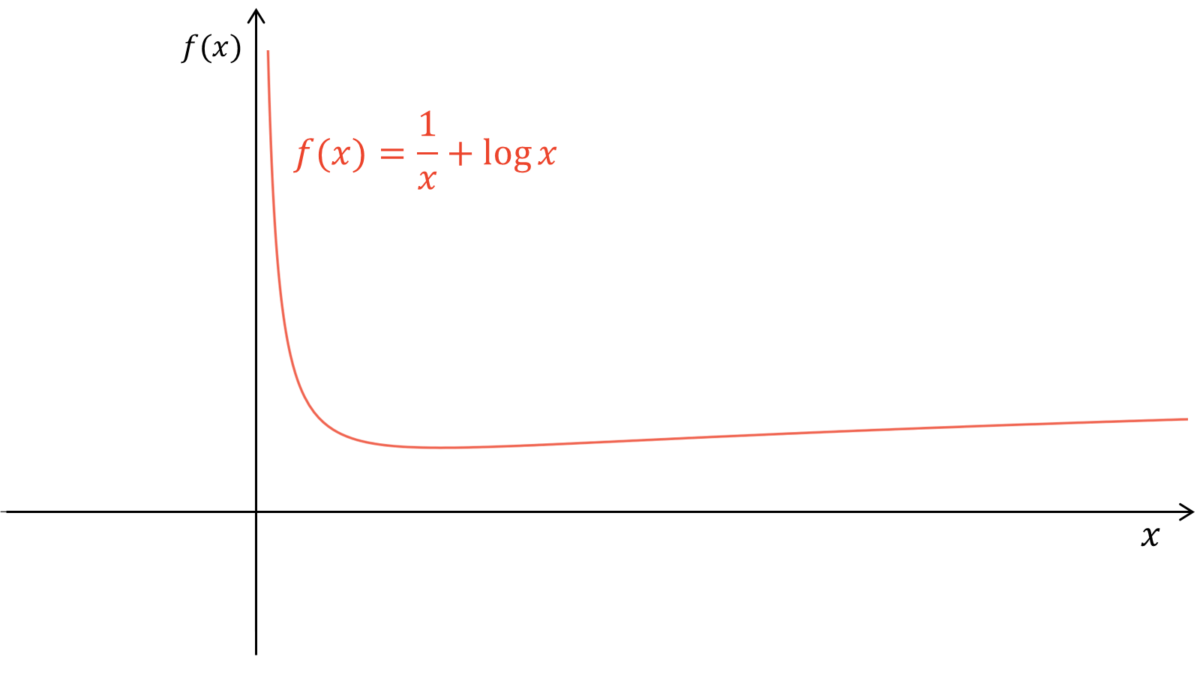
$\log x$の定義域は$x>0$であることから，ユークリッド距離基準の更新式の導出過程とは異なり，$h_{l,m}$と$u_{m,n}$は非負であるという制約は既に課せられています。

まずは，$G_{\IS}$の$\mH$に関する導関数が$0$になるという条件を考えます。

これを整理すると，以下が得られます。

ただし，$h_{l,m}>0$を利用しました。次に，$G_{\IS}$の$\mU$に関する導関数が$0$になるという条件を考えます。

これを整理すると，以下が得られます。

ただし，$u_{m,n}>0$を利用しました。$\mLambda$と$\valpha$はこちら側の都合で勝手に導入した補助変数ですので，最後の仕上げとして式($\ref{IS_等号成立1}$)，式($\ref{IS_等号成立2}$)は式($\ref{IS_h}$)，式($\ref{IS_u}$)に代入して$\lambda_{l,m,n}$と$\alpha_{l,n}$を消去した形にしてあげます。以上より，冒頭の更新式が示されました。

生成モデルによる解釈

ユークリッド二乗距離，$\I$ダイバージェンス，板倉斎藤擬距離を乖離度とするNMFは，観測行列の要素$y_{l,n}$が$x_{l,n}$を平均とした正規分布，ポアソン分布，指数分布に従って独立に生成されたと仮定した場合の$\mH, \mU$の最尤推定問題と等価になります。ここで，以降の議論を簡潔に行うため，

を満たす$\vx_{n}$を定義します。このとき，NMFの最適化問題($\ref{最適化問題}$)はつぎのように表されます。

以下では，各種乖離度に基づくNMFはある確率分布に対する最尤推定問題と等価になることを示します。

ユークリッド二乗距離基準

観測行列の要素$y_{l,n}$が平均$x_{l,n}$，分散$\sigma^{2}$の正規分布から独立に生成されること，すなわち

を仮定します。このとき，対数尤度を$L_{\N}$とおくと，

と表されます。$D_{\EU}$の等号を反転させると，$D_{\EU}$は$L_{\N}$と等価になります。したがって，対数尤度$L_{\N}$の最大化はユークリッド二乗距離$D_{\EU}$の最小化と等価になります。

Iダイバージェンス基準

観測行列の要素$y_{l,n}$が$x_{l,n}$をパラメータとしたポアソン分布から独立に生成されること，すなわち

を仮定します。ただし，ポアソン分布の実現値は整数値であることから，$y_{l,n}$は非負の整数値に限定されることに注意してください。このとき，対数尤度を$L_{\Po}$とおくと，

と表されます。$D_{\I}$において，定数である観測値$y_{l,n}$に関する項を除いて等号を反転させると，$D_{\I}$は$L_{\Po}$と等価になります。したがって，対数尤度$L_{\Po}$の最大化は$\I$ダイバージェンス$D_{\I}$の最小化と等価になります。

板倉斎藤擬距離基準

観測行列の要素$y_{l,n}$が$x_{l,n}$を尺度母数とした指数分布から独立に生成されること，すなわち

を仮定します。ただし，$x_{l,n}$は$0$とならないことを仮定し，指数分布のパラメータの逆数を尺度母数としている点に注意してください。このとき，対数尤度を$L_{\Exp}$とおくと，

と表されます。$D_{\IS}$において，定数である観測値$y_{l,n}$に関する項と定数$1$を除いて等号を反転させると，$D_{\IS}$は$L_{\Exp}$と等価になります。したがって，対数尤度$L_{\Exp}$の最大化は板倉斎藤擬距離$D_{\IS}$の最小化と等価になります。

上述の通り，$\beta$ダイバージェンス，Bregmanダイバージェンスを乖離度とするNMFは，それぞれ観測行列の要素$y_{l,n}$が$x_{l,n}$を平均としたTweedie分布，指数分布族に従って独立に生成されたと仮定した場合の$\mH, \mU$の最尤推定問題と等価になります。

実装

本章では，ユークリッド二乗距離基準・$\I$ダイバージェンス基準・板倉斎藤擬距離基準のNMFの実装方法をお伝えしていきます。簡単のため，今回は下記のパラメータを仮定します。

なお，Githubで公開している実装では，dockerを用いてNMFが実行できる環境を用意しています。上記パラメータを含め，さまざまなパラメータをdocker-compose.ymlで管理しています。

ソースコードのコメントは英語で書いています。これはGithubで公開する際に，外国の方々にも参考にしていただきたいからです。また，コメント規則であるdocstringはGoogleスタイルを利用しています。

ここからは，以下の形式でメソッド単位で解説を行っていきます。

# ソースコード

データの準備

以下では，NMFを適用するデータを生成していきます。

import numpy as np
import matplotlib.pyplot as plt
import sys

標準的なライブラリをインポートします。

Y = np.random.randint(1, 10, (10, 10)) # [1,10]の値を取る(10,10)サイズの行列を分解する

適当な近似行列を定義します。ただし，GitHubで公開している実装では，docker-compose.ymlによって，与えたパラメータにしたがって観測行列Yを自動生成する仕組みになっています。

NMFクラスの定義

class NMF():

ここからは，NMFクラスを定義していきます。

コンストラクタ

    def __init__(self, Y, M):
        """コンストラクタ

        Args:
            Y (numpy ndarray): (N, L)サイズの観測行列
            M (int): 基底の数

        Returns:
            None.

        Note:
            eps (float): オーバーフローとアンダーフローを防ぐための微小量
        """
        self.eps = np.spacing(1)
        self.Y = Y 
        self.M = M

コンストラクタでは，観測行列Yと基底数Mを初期化します。また，ゼロ除算やゼロの対数によるオーバーフローとアンダーフローを防ぐための微小量epsも定義します。

パラメータ初期化メソッド

    def init_params(self):
        """パラメータ初期化メソッド

        Args:
            None.

        Returns:
            None.
        """
        self.cost_tmp = 10**6 # 適当に大きな数
        self.cost = np.array([self.cost_tmp]) # 乖離度を記録するための配列
        self.cnt_iteration = 1 # イテレーション回数を記憶しておく変数

コンストラクタとは別に，パラメータ初期化メソッドを定義します。これは，一つのクラスで複数の乖離度に基づく更新を行うためです。

行列初期化メソッド

    def init_matrix(self):
        """行列初期化メソッド

        Args:
            None.
        Returns:
            None.
        """
        self.H = np.random.uniform(low=1, high=10, size=(self.Y.shape[0], self.M)) # (L, M)
        self.U = np.random.uniform(low=1, high=10, size=(self.M, self.Y.shape[1])) # (M, N)
        self.X = self.H @ self.U

パラメータ初期化メソッドと同様に，パラメータ初期化メソッドを定義します。

乖離度計算メソッド

    def EU_divergence(self):
        """ユークリッド二乗距離計算メソッド

        Args:
            None.
        Returns:
            None.
        """
        self.cost_tmp = ((self.X-self.Y)**2).mean()

    def I_divergence(self):
        """Iダイバージェンス計算メソッド

        Args:
            None.
        Returns:
            None.
        """
        self.cost_tmp = (self.Y*np.log(self.Y/(self.X+self.eps)+self.eps)-self.Y+self.X).mean()

    def IS_divergence(self):
        """板倉斎藤擬距離計算メソッド

        Args:
            None.
        Returns:
            None.
        """
        self.cost_tmp = (self.Y/(self.X+self.eps)-np.log(self.Y/(self.X+self.eps)+self.eps)-1).mean()

各種乖離度を計算するメソッドを定義します。ここに他の乖離度を定義することも可能です。

更新メソッド

    def EU_update(self):
        """ユークリッド二乗距離基準のNMF更新式計算メソッド

        Args:
            None.
        Returns:
            None.
        """
        self.H *= (self.Y @ self.U.T) / ((self.H @ self.U) @ self.U.T + self.eps)
        self.U *= (self.Y.T @ self.H).T / ((self.H @ self.U).T @ self.H + self.eps).T

    def I_update(self):
        """Iダイバージェンス基準のNMF更新式計算メソッド

        Args:
            None.
        Returns:
            None.
        """
        self.H *= ((self.Y / ((self.H @ self.U) + self.eps)) @ self.U.T)  / (self.U.sum(axis=1, keepdims=True).T + self.eps)
        self.U *= ((self.Y / ((self.H @ self.U) + self.eps)).T @ self.H).T  / (self.H.sum(axis=0, keepdims=True).T + self.eps)

    def IS_update(self):
        """板倉斎藤擬距離基準のNMF更新式計算メソッド

        Args:
            None.
        Returns:
            None.
        """
        self.H *= np.sqrt(((self.Y / ((self.H @ self.U)**2 + self.eps)) @ self.U.T) / (self.U @ (1/((self.H @ self.U) + self.eps)).T + self.eps).T)
        self.U *= np.sqrt(((self.Y / ((self.H @ self.U)**2 + self.eps)).T @ self.H).T / (self.H.T @ (1/((self.H @ self.U) + self.eps)) + self.eps))

各種乖離度に対する解析的な更新式を定義します。特に，ゼロ除算やゼロの対数によるオーバーフローとアンダーフローを防ぐためにコンストラクタで定義した微小量を利用する点に注意してください。

学習メソッド

    def execute(self, n_iteration, divergence):
        """学習メソッド

        Args:
            n_iteration (int): 学習回数の上限
            divergence (String): "EU", "I", "IS"のうちいずれかの乖離度
        Returns:
            None.
        """
        while True:
            if (divergence=="EU"):
                self.EU_update()
                self.EU_divergence()
            elif (divergence=="I"):
                self.I_update()
                self.I_divergence()
            elif (divergence=="IS"):
                self.IS_update()
                self.IS_divergence()
            else:
                print("Please select from EU, I, IS for the divergence.")
                sys.exit(1)

            if (self.cnt_iteration >= n_iteration or self.cost_tmp > self.cost[-1]):
                print(f"====={self.cnt_iteration}回目でcostが悪化したため終了=====")
                break
            else:
                self.X = self.H @ self.U
                self.cost = np.append(self.cost, self.cost_tmp)
                self.cnt_iteration += 1

上で定義した各種メソッドを利用して，学習を行うメソッドを定義します。DNNの確率的勾配降下法とは異なり，NMFでは解析的な解に基づく更新式を繰り返し適用していきますので，本来であれば学習回数のみを指定してあげればよいのです。しかし，今回は「更新回数の上限に到達した」または「コストである乖離度が悪化した」場合に学習を停止させるようにしています。後者を入れているのは，微小量とはいえゼロ除算やゼロの対数に近い演算を行うことによる情報の欠落や，初期値のランダム性による局所解への収束が考えられるためです。

乖離度の減少過程描画メソッド

    def visualize_cost(self):
        """乖離度減少過程可視化メソッド

        Args:
            None.
        Returns:
            None.
        """
        index = np.arange(self.cost.size-2)
        plt.figure(figsize=(16,9))
        plt.rcParams["font.size"] = 18
        plt.plot(index, self.cost[2:], color=(0.93,0.27,0.17))

乖離度の減少過程をグラフ化するメソッドを定義します。ここではplotしていますが，GitHubで公開している実装ではコンテナとvolumeマウントを行い，画像を保存しています。

観測行列と近似行列の描画メソッド

    def visualize_heatmap(self):
        """観測行列と近似行列の描画メソッド

        Args:
            None.
        Returns:
            None.
        """
        fig, axes = plt.subplots(1, 2, figsize=(16,9))
        fig.subplots_adjust(wspace=0.1, hspace=0.1)
        axes[0].imshow(self.Y, cmap="inferno")
        axes[0].axis("off")
        axes[1].imshow(self.X, cmap="inferno")
        axes[1].axis("off")
        plt.show()

観測行列と近似行列をヒートマップで可視化するメソッドを定義します。このメソッドを通して，NMFがどれだけ精度良く加速行列を近似できたかを定性的に観察することができます。

パラメータの設定

M = 5 # 基底の数は5
n_iteration = 100 # 更新回数は100

各種パラメータを設定します。

NMFクラスのインスタンス化

model = NMF(Y, M)

上で定義したNMFクラスをインスタンス化しましょう。

NMFの実行

上でも言及した通り，NMFでは適切でない初期値を与えると局所解に収束してしまう可能性があります。そこで，今回は「パラメータで設定した更新回数の上限に初めて達した場合」の結果を抽出することにします。

ユークリッド二乗距離基準

while True:
    model.init_matrix()
    model.init_params()
    model.execute(n_iteration, "EU")
    if model.cnt_iteration == n_iteration:
        break
model.visualize_cost()
model.visualize_heatmap()

ユークリッド二乗距離基準の乖離度減少過程は以下のようになりました。

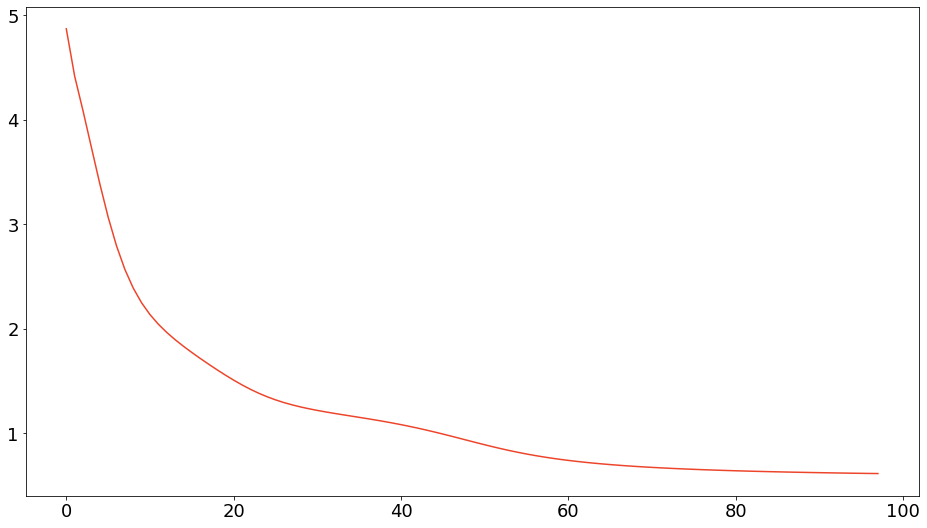
ユークリッド二乗距離基準の観測行列と近似行列の可視化は以下のようになりました。

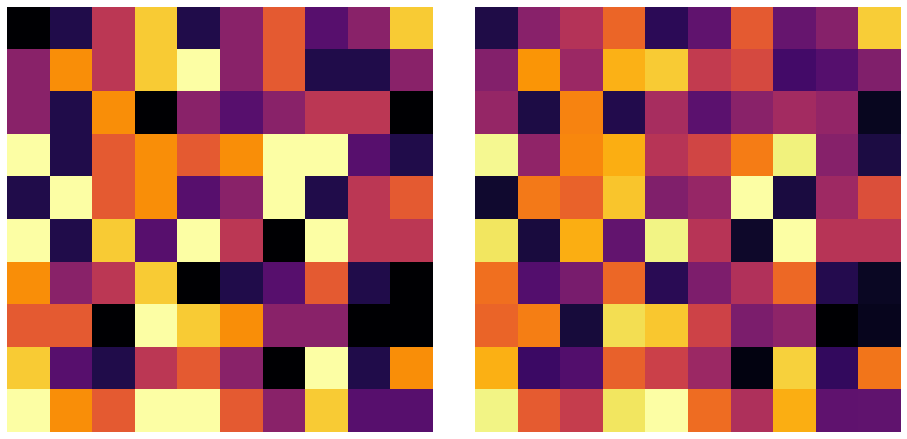
Iダイバージェンス基準

while True:
    model.init_matrix()
    model.init_values()
    model.execute(n_iteration, "I")
    if model.cnt_iteration == n_iteration:
        break
model.visualize_cost()
model.visualize_heatmap()

$\I$ダイバージェンス基準の乖離度減少過程は以下のようになりました。

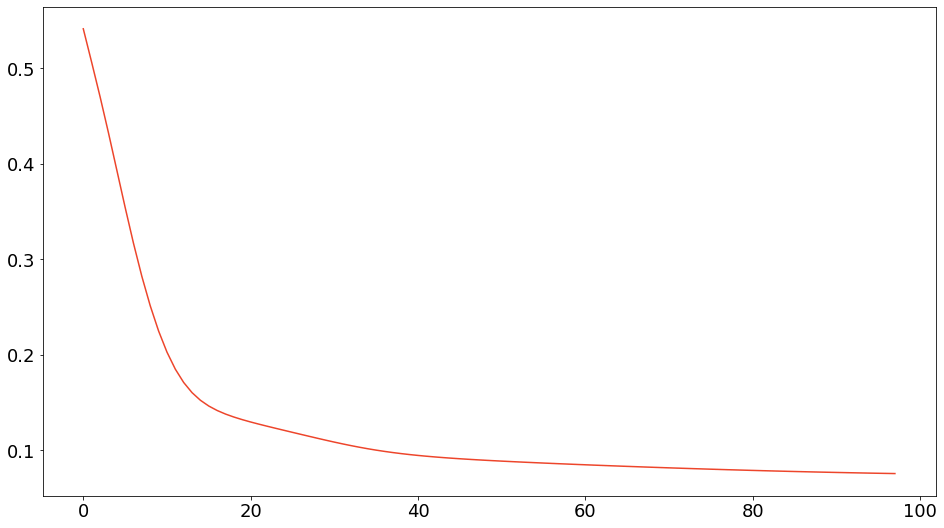
$\I$ダイバージェンス基準の観測行列と近似行列の可視化は以下のようになりました。

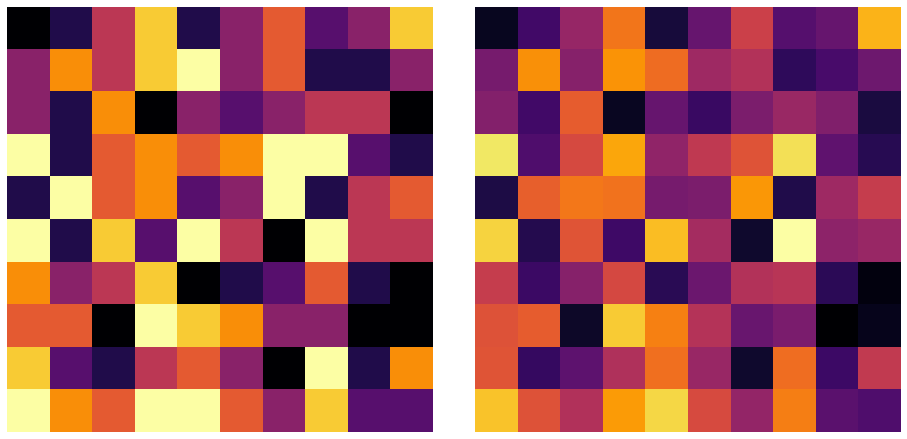
板倉斎藤擬距離基準

while True:
    model.init_matrix()
    model.init_values()
    model.execute(n_iteration, "IS")
    if model.cnt_iteration == n_iteration:
        break
model.visualize_cost()
model.visualize_heatmap()

板倉斎藤擬距離基準の乖離度減少過程は以下のようになりました。

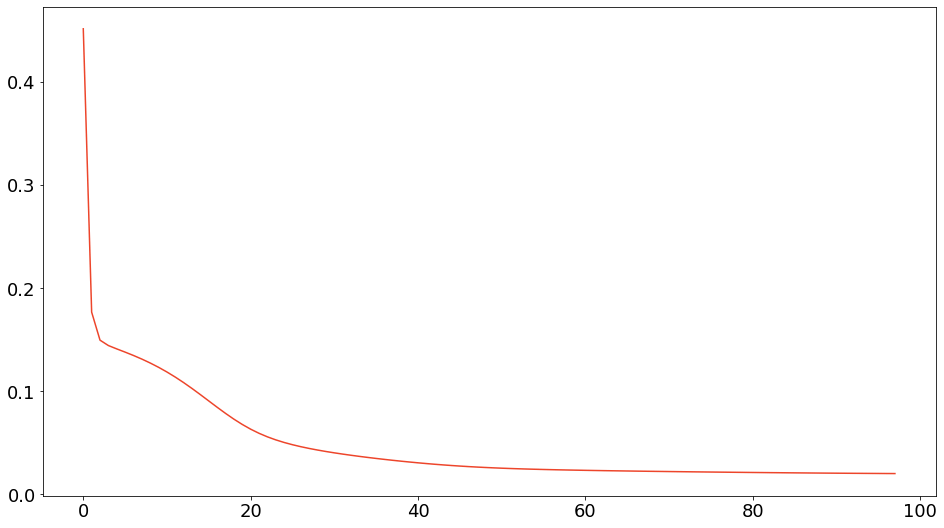
板倉斎藤擬距離基準の観測行列と近似行列の可視化は以下のようになりました。

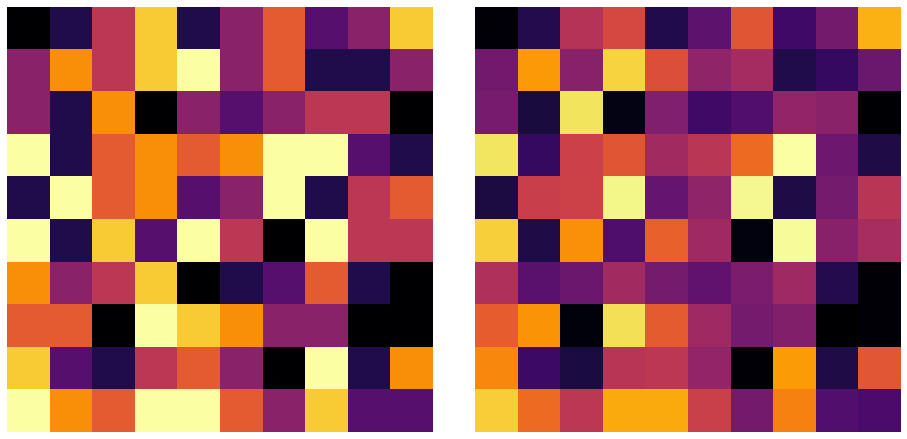
おわりに

深層学習（DNN：deep neural networks）の発展が凄まじい昨今においても，NMFにはDNNを用いた手法と匹敵するポテンシャルがあります。数学的な妥当性の担保が難しいDNNベースの手法とは対照的に，確率的生成モデルによる裏付けが可能なNMFを用いた研究には，地に足つけた取り組みが多い印象があります。特に音源分離の分野では，いまだにNMFに基づく手法の性能が高いことが知られています。

しかしながら，NMFには残された課題も数多く存在します。まず，モデルの緻密さを表す基底数が自明でないため，状況によって設定する必要があります [8]。さらに，自明なパラメータが多数存在することからNMFの最適化問題はNP困難であることが知られています [9]。実際，NMFの分解には一意性がなく [10]，初期値に依存して意図しない解に収束することが多いです。これらの課題を克服し，DNNベースの手法を理論・性能の両側面から凌駕するような研究が今後積極的になされることを期待しています。

NMFを音響信号の観測スペクトログラムに適用する場合には，スペクトルは加法的であるという仮定と周波数成分比が時不変でゲインのみが時間変化するという仮定をおいています。これらの仮定は実際には成り立たないため，NMFを複素領域に拡張してモデルとしての妥当性を担保する複素NMF [11] が提案されています。

参考文献

[1] Lee+. Learning the Parts of Objects by Non-negative Matrix Factorization. Nature, 1999.
[2] Lee+. Algorithms for Non-negative Matrix Factorization. NeurIPS, 2001.
[3] Xu+. Document Clustering Based on Non-negative Matrix Factorization. ACM, 2003.
[4] Smaragdis+. Supervised and Semi-supervised Separation of Sounds from Single-channel Nixtures. ICA, 2007.
[5] King+. Optimal Cost Function and Magnitude Power for NMF-based Speech Separation and Music Interpolation. MLSP, 2012.
[6] Fitzgerald+. On the Use of the Beta Divergence for Musical Source Separation. In IET, 2009.
[7] Nakano+. Convergence-guaranteed Multiplicative Algorithms for Nonnegative Matrix Factorization with β-divergence. MLSP, 2010.
[8] Tan+. Automatic Relevance Determination in Nonnegative Matrix Factorization with the/spl beta/-divergence. TPAMI, 2012.
[9] Vavasis. On the Complexity of Nonnegative Matrix Factorization. SIAM, 2010.
[10] Huang+. Non-negative Matrix Factorization Revisited: Uniqueness and Algorithm for Symmetric Decomposition. TSP, 2013.
[11] Kameoka+. Complex NMF: A New Sparse Representation for Acoustic Signals. ICASSP, 2009.