本記事は機械学習の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
Kermack-McKendrickのSIRモデルとは
Kermack-McKendrickのSIRモデルは「感受性(susceptible)個体」「感染(infectious)個体」「免疫のある(removed)個体」の3者を対象とした収支式の一種です。以下にKermack-McKendrickのSIRモデルの概要図を示します。
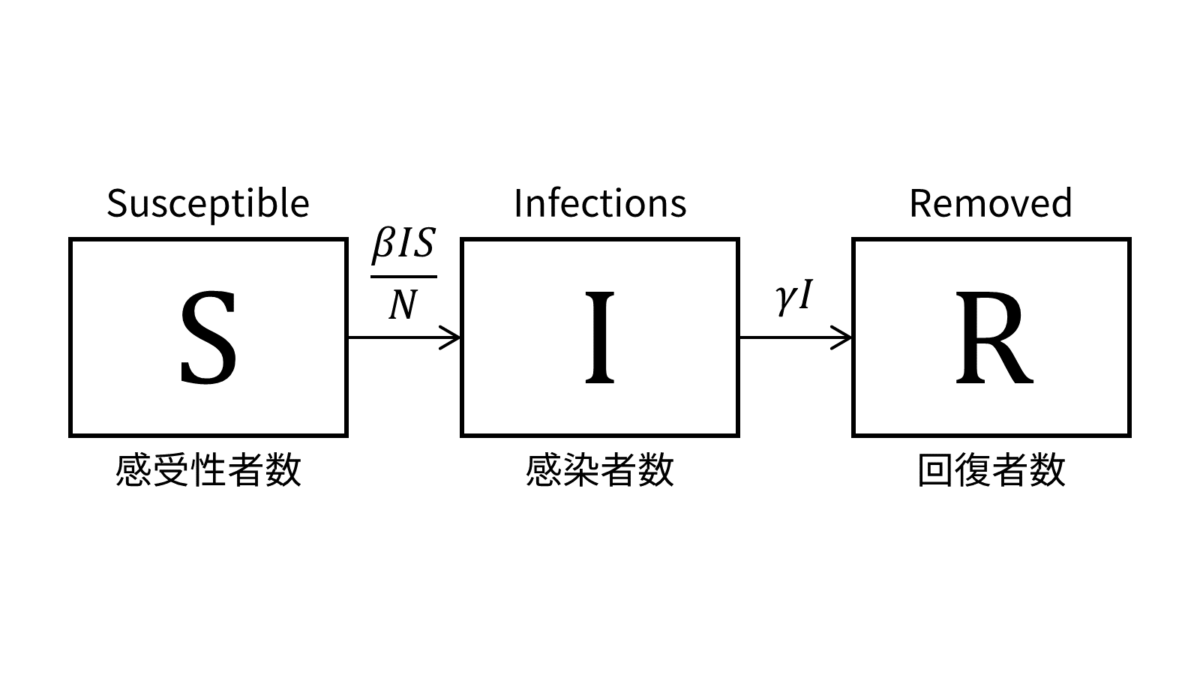
注意すべき点として,Kermack-McKendrickのSIRモデルは感染の流行過程のモデルとしては非常に単純なものであり,例えば一回感染した人が再び感染するような循環や潜伏期間などには対応できないことが指摘できます。
定式化
具体的には,以下の常微分方程式を考えます。
\frac{d S}{d t} &=-\frac{\beta I S}{N} \label{eq:1}\\[0.7em]
\frac{d I}{d t} &=\frac{\beta I S}{N}-\gamma I \label{eq:2}\\[0.7em]
\frac{d R}{d t} &=\gamma I \label{eq:3}
\end{align}
ここで,$S$は感受性者数,$I$は感染者数,$R$は回復(死亡)者数,$N$は総人口,$\beta$は感染率,$\gamma$は回復(死亡)率を表します。また,以下で定義される$R_{0}$は基本再生産数と呼ばれ,感染率と回復率の比を表しており「一人の感染者がどれだけの二次感染者を産み出すか」を表しています。
R_0 &= \frac{\beta}{\gamma}
\end{align}
Kermack-McKendrickのSIRモデルは,式(\ref{eq:1})と式(\ref{eq:3})を連立させて変数分離形の微分方程式を解くことで解析的な解が得られます。なお,$S+I+R=N$という制約式があることから,式(\ref{eq:1})と式(\ref{eq:3})を連立させることで,同時に式(\ref{eq:2})も考えていることになることに注意しましょう。
実装
本記事では,pythonのscipyライブラリを利用して上記の微分方程式を解きます。なお,対象都市は京都市とします。また,パラメータ設定に関しては以下の三条件を考えます。
- 2020/10/28時点
- 基本再生産数が多い場合
- 初期感染者数が多い場合
それぞれについて,横軸を時間(三年間),縦軸を個体数としたグラフを描画することで,Kermack-McKendrickのSIRモデルについて考察を加えていきます。最初に実装の概要をお伝えしていきます。
ソースコード
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
cm = plt.get_cmap("Dark2")
# odeintに渡す関数
def SIRmodel(v, t, beta, gamma, N):
S = v[0]
I = v[1]
R = v[2]
dSdt = - beta*S*I/N
dIdt = beta*S*I/N - gamma*I
dRdt = gamma*I
return [dSdt, dIdt, dRdt]
# 現状のパラメータ設定
t_max = 365*3
dt = 1
R0 = 1.06
PR = 1408/30375
beta = PR
gamma = beta / R0
N = 1475000
I_0 = 55/PR
R_0 = 1332
S_0 = N - I_0 - R_0
initial_vaules = [S_0, I_0, R_0]
T = np.arange(0, t_max, dt)
parameters = (beta, gamma, N)
R0 = beta/gamma
# odeintに関数と初期値を渡して計算してもらう
res = odeint(SIRmodel, initial_vaules, T, parameters)
# cmapを変えて可視化したいのでfor文を回す
for i in range(len(res[0])):
plt.plot(T, res[:,i], color=cm(i))
plt.legend(["Susceptible", "Infectious", "Removed"])2020/10/28時点
パラメータは以下のように設定します。ここでは,感染率が陽性率と同等程度と近似することにします。
- $t_{\mathrm{max}}$:$365 \times 3$(三年間)
- $dt$:$1$(一日ごと)
- $R_0$:$1.06$(2020/10/28時点における京都市の基本再生産数)
- $N$:$1475000$(京都市総人口)
- $\mathrm{PR}$:$1408/30375$(陽性率)
- $\beta$ :$\mathrm{PR}$(仮定より)
- $\gamma$:$\beta$/$R_0$ (回復率)
- $I_0$:$55/\mathrm{PR}$(入院者と陽性率より概算)
- $R_0$:$1332$(累積感染者数として概算)
- $S_0$:$N - I_0 - R_0$(総人口が$N$であることから計算)
すると,描画されたグラフは以下の図のようになります。
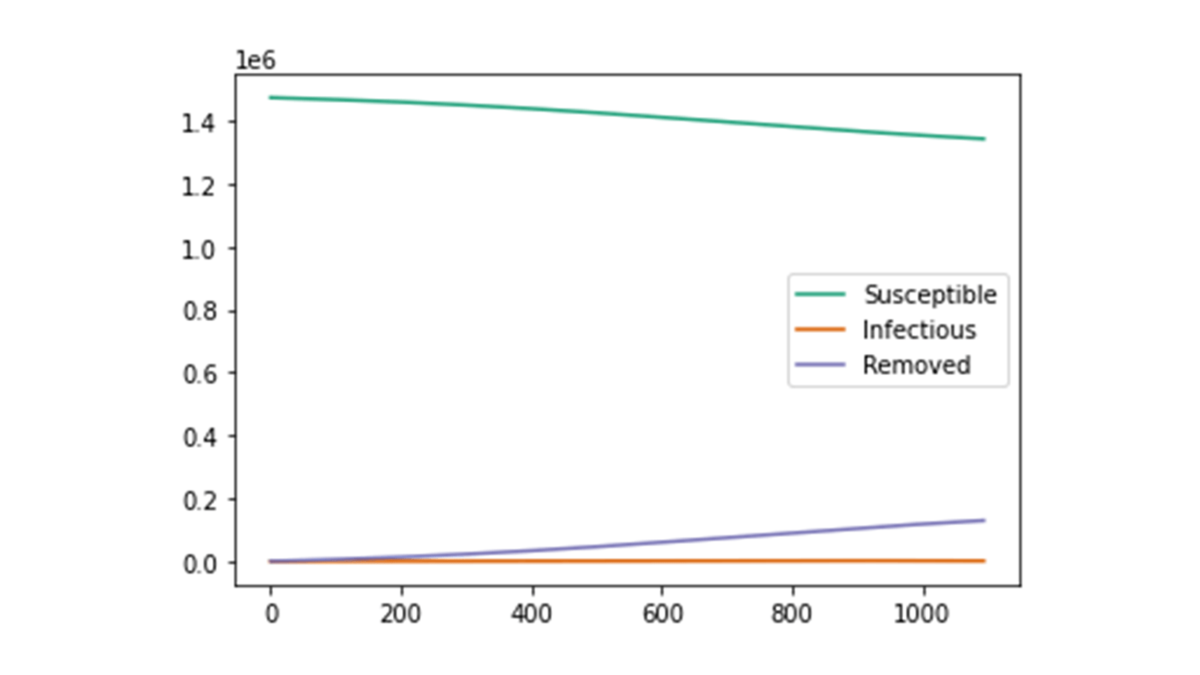
このグラフから,三年間で感染者数が爆発的に増えるということはなく,徐々に感染者数が増えていくことが分かります。
基本再生産が多い場合
基本的なパラメータは10/28と同様に設定します。ただし,本節では基本再生産が$2$の場合を考えます。すると,描画されたグラフは以下の図のようになります。
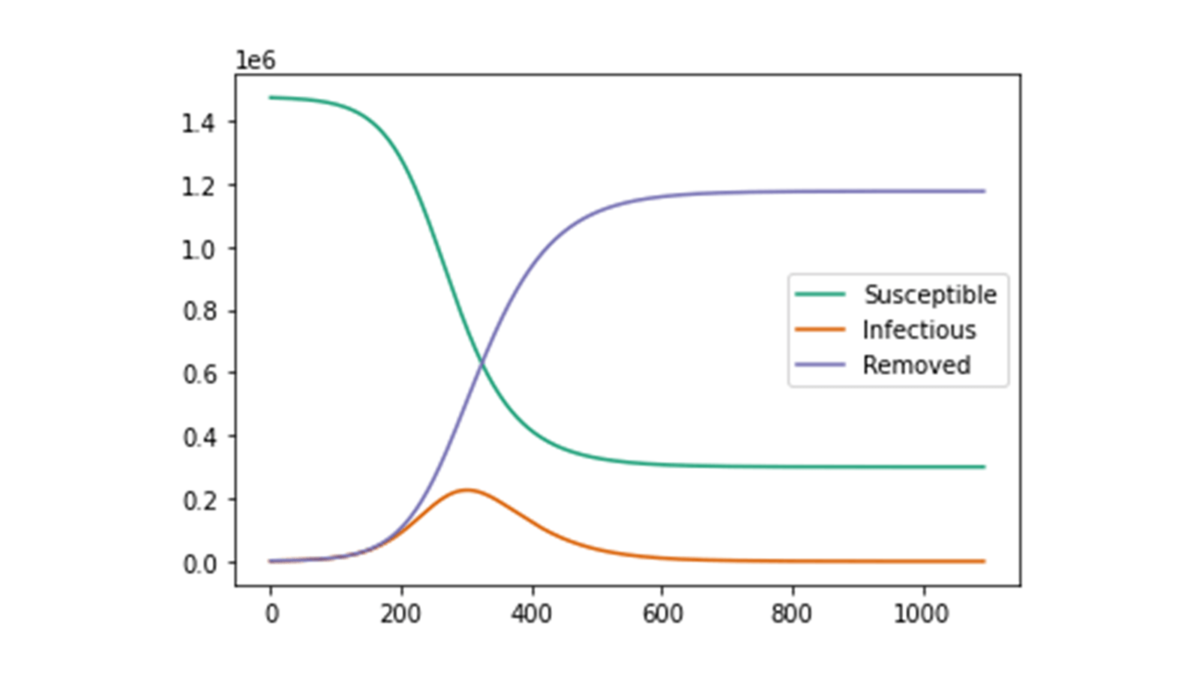
このグラフから,基本再生産数が2に増えるだけで,感染者数が約一年後から爆発的に伸び始め,二年後にはほぼ収束してしまうことが読み取れます。最終的な免疫獲得者および死亡者数の合計は,$120$万人に到達します。基本生産数はKermack-McKendrickのSIRモデルにおける振る舞いを定める大きな要因であることが分かりますね。つまり,自粛要請も非常に妥当な政策であったということです。
初期感染者数が多い場合
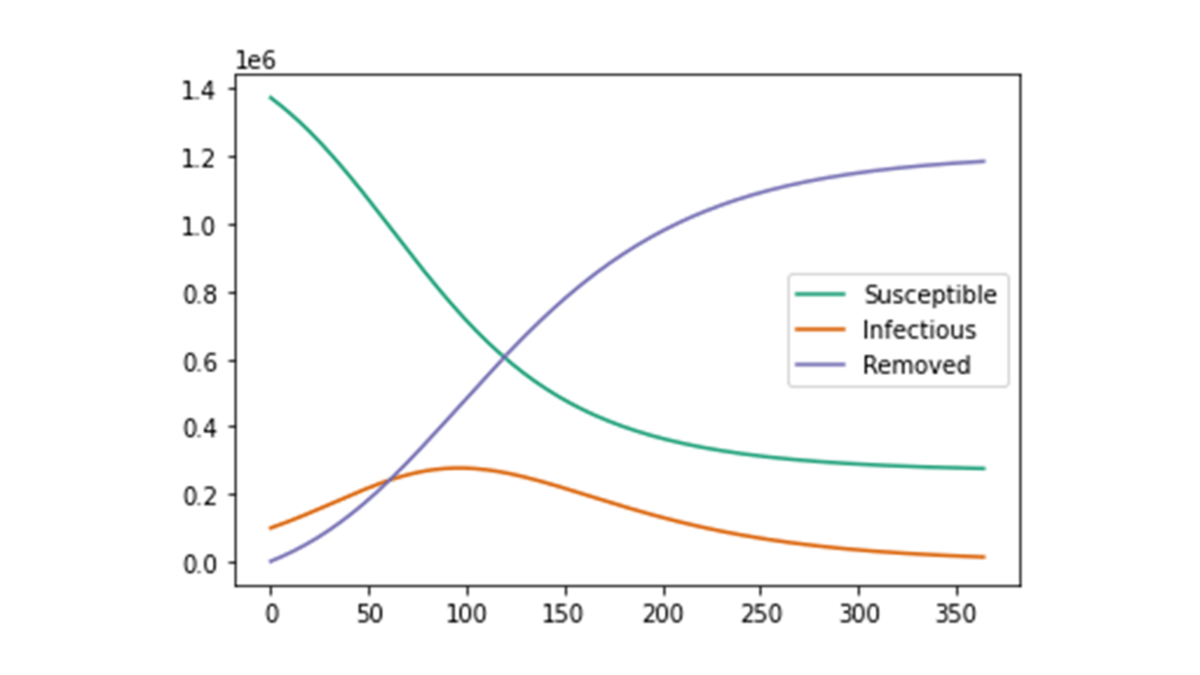
基本的なパラメータは10/28と同様に設定します。ただし,本節では$I_0$が$10$万の場合を考えます。すると,描画されたグラフは以下の図のようになります。
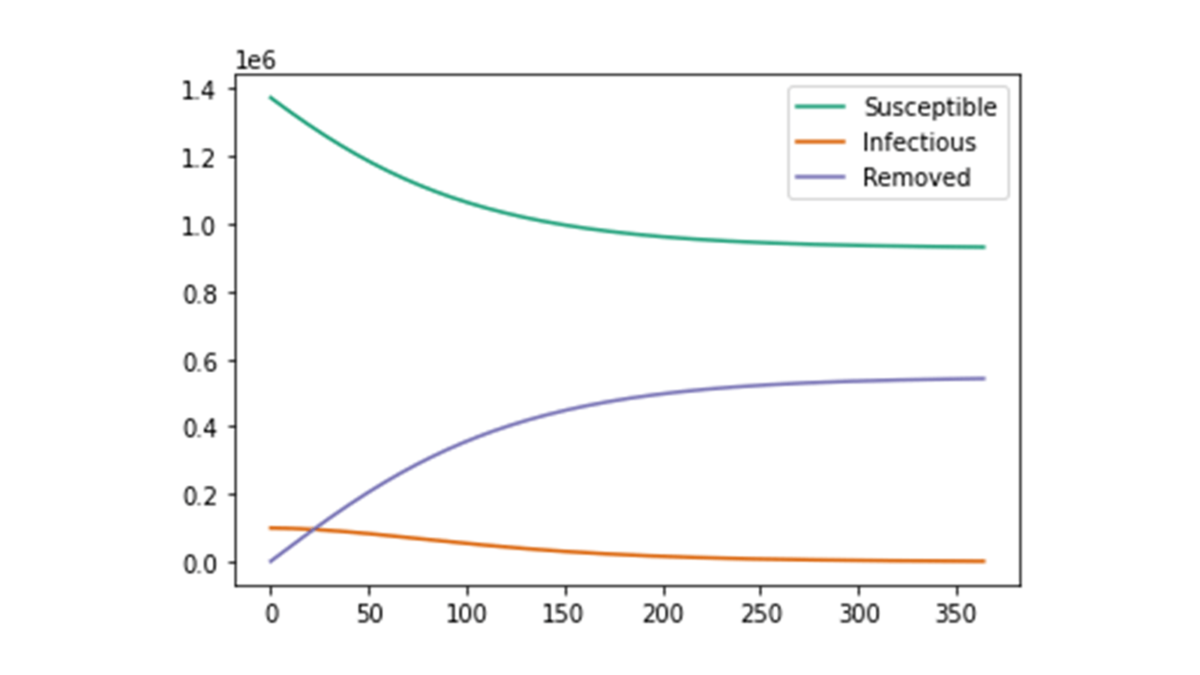
このグラフから,10/28の状況下と比べて,感受性者数が減っていく傾向にあることが分かります。これは,基本再生産数が多い場合におけるピーク後の形と一致しており,今回の初期値$I_0=100000$がすでにKermack-McKendrickのSIRモデルにおけるピーク後の値を与えていたことを示唆しています。実際,「基本生産数が多い場合」の図において「Infectious」の数が$100000$の部分はピークの直前・直後に位置しており,基本再生産数が10/28時点で$1.06$と比較的低いため,今回の「初期感染者数が多い場合」はピーク後のような振る舞いを示したものと考えられます。実際,同様のパラメータ設定において基本再生産数を$2$に設定すると,以下の図のようにピーク直前からの振る舞いを示しています。


コメント