本記事では,数学検定1級で頻出のトピックについてまとめていきます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
数検1級における複素解析の扱い
出題頻度は少ないですが,数検1級では「基本的な複素解析」が試験範囲に含まれています。「基本的」と銘打っていることもあり,出題されるとしても1次試験の計算テクニックとして狙われることになるでしょう。具体的には,留数定理を用いると計算が楽になる(もしくは留数定理を用いないと解析的に解けない)積分が出題される可能性があります。逆に言えば,例えばコーシー・リーマンの関係式を知らないと解けない正則性の証明や,解析接続に関する高度なトピックが出題される可能性は非常に低いと考えられます。そこで,本項では「積分計算を楽にするテクニック」に振り切り,留数定理の扱いを確認していきます。
準備
以下では,留数定理を説明するために必要な用語の定義を確認します。
単純閉曲線とは
交差せずに出発点に戻ってくる曲線のことを指します。数字の「8」を一筆書きするときのように,筆が交差せずに1周する曲線のことを単純閉曲線といいます。
「区分的になめらか」とは
いくつかの部分に分けると各々の部分は微分可能であり,導関数が連続であるような性質のことを指します。部分的にこの性質を満たせばよいため,例えば区間の端点においては折れ曲がったり導関数が不連続であったりしてもよいということです。
正則とは
複素関数$f(z)$が$z=z_{0}$微分可能で導関数が連続なとき,$f(z)$は$z=z_{0}$にいて正則といいます。
孤立特異点
その近くに他の特異点が存在しない特異点のことを指します。特異点とは,複素関数$f(z)$が$z_{0}$において正則でないが$z_{0}$の近傍では正則となるような点$z_{0}$のことを指します。
線積分・周回積分とは
複素関数を曲線に沿って積分することを線積分といい,線積分のうち閉曲線に沿ったものを周回積分といいます。
補足
線積分は実数上の積分と同じように複素数の微小変化量の総和に対する極限
\int_{C}f(z)dz &= \lim_{N\to\infty}\sum_{i=0}^{N-1}f(z_{i})\Delta z_{i}
\end{align}
を考えればよいですが,実用上は
\int_{C}f(z)dz &= \int_{a}^{b}f(z(t))\frac{dz}{dt}
\end{align}
のように積分路のパラメータ表示を利用します。
ローラン展開とは
テイラー展開を特異点でも扱えるように拡張したものがローラン展開です。数検1級において計算テクニックとして留数定理を利用する場合,下記の内容は完璧に理解しなくてもよく,流し見程度でも大丈夫です。
$f(z)$が$0{<}|z-\alpha|{<}R$で正則ならば,$D{=}\{z\in\mC\mid r_{1}{\leq}|z-\alpha|{\leq}r_{2}\}~(0{<}r_{1}{<}r_{2}{<}R)$上で
f(z) &= \sum_{n=-\infty}^{\infty}c_{n}(z-\alpha)^{n}
\end{align}
のようにべき級数展開できる。ただし,各係数は$0<r<R$を満たす任意の実数$r$を用いて
c_{n} &= \frac{1}{2\pi i}\oint_{|z-\alpha|=r}\frac{f(z)}{(z-\alpha)^{n+1}}dz
\end{align}
と表される。$\alpha$を$f(z)$の孤立特異点といい,ローラン展開の$z-\alpha$の負のべき乗部分
\sum_{n=-\infty}^{-1}c_{n}(z-\alpha)^{n}
\end{align}
を孤立特異点$\alpha$における$f(z)$の主要部という。
$D{=}\{z\in\mC\mid r_{1}{\leq}|z-\alpha|{\leq}r_{2}\}~(0{<}r_{1}{<}r_{2}{<}R)$は「ドーナツで切り落とす真ん中の穴は$z=\alpha$に限りなく近づけることができ,$R$はどこまでも大きくすることができる」という意味です。なお,ローラン展開の証明はコーシーの積分定理に基づきます。本項では留数定理を証明なしで与えますが,留数を定義するためにはローラン展開の説明が必要なので記載しています。
極とは
主要部が有限級数のとき,$c_{-m}\neq 0$として
f(z) &= \frac{c_{-m}}{(z-\alpha)^{m}}+\cdots+\frac{c_{-1}}{z-\alpha}+\sum_{n=0}^{\infty}c_{n}(z-\alpha)^{n}
\end{align}
となる場合,$\alpha$を$f(z)$の$m$位の極という。
本当にざっくり捉えるならば,分母の次数が$m$であれば大抵$m$次の極です。
留数とは
$f(z)$の$z=\alpha$におけるローラン展開における$C_{-1}$を留数といい,$\Res(f(z),\alpha)$で表す。ヘビサイドの展開定理と同様すると,点$\alpha$が$k$位の極であるとき,
\Res(f(z),\alpha)
&= \frac{1}{(k-1)!}\lim_{z\to\alpha}\frac{d^{k-1}}{dz^{k-1}}\left\{(z-\alpha)^{k}f(z)\right\}\label{留数の求め方}
\end{align}
のように計算できる。
この計算が留数定理を計算テクニックたらしめる真髄です。複雑な積分計算を非常に簡単に計算することが可能になります。
$1$位の極における留数の求め方
式($\ref{留数の求め方}$)により,$1$位の極は
\Res(f(z),\alpha) &= \lim_{z\to\alpha}(z-\alpha)f(z)\label{留数_1位の極_基本}
\end{align}
で求められる。特に,$p(\alpha)\neq 0$および$q(\alpha)=0$なる$p,q$を用いて$f(z)=p(z)/q(z)$と表されるとき,分母の$q(z)$を$\alpha$のまわりでテイラー展開することにより,$q(\alpha)=0$に注意すると
\Res(f(z),\alpha)
&= \lim_{z\to\alpha}\frac{(z-\alpha)p(z)}{q(\alpha)+q^{\prime}(\alpha)(z-\alpha)+q^{\prime\prime}(\alpha)(z-\alpha)^{2}/2+\cdots}\\[0.7em]
&= \lim_{z\to\alpha}\frac{(z-\alpha)p(z)}{q^{\prime}(\alpha)(z-\alpha)+q^{\prime\prime}(\alpha)(z-\alpha)^{2}/2+\cdots}\\[0.7em]
&= \lim_{z\to\alpha}\frac{p(z)}{q^{\prime}(\alpha)+q^{\prime\prime}(\alpha)(z-\alpha)/2+\cdots}
= \frac{p(\alpha)}{q^{\prime}(\alpha)}
\end{align}
が得られる。したがって,$(z-\alpha)f(z)$の計算が面倒な場合には
\Res(f(z),\alpha)
&= \frac{p(\alpha)}{q^{\prime}(\alpha)}\label{留数_1位の極_微分}
\end{align}
を用いて留数を求めるとよい。
留数定理
関数$f(z)$は区分的になめらかな単純閉曲線$C$の内部に孤立特異点$\alpha_{1},\ldots,\alpha_{n}$を持ち,これらを除いて正則であるとする。このとき,
\oint_{C}f(z)dz &= 2\pi i\sum_{i=1}^{n}\Res(f,\alpha_{i})
\end{align}
が成り立つ。ただし,$\Res(f,\alpha_{i})$は$f(z)$の$z=\alpha_{i}$での留数とする。
ぱっと見よく理解できないと思いますので,例題で留数定理の使い方を把握し,そこからボトムアップで留数の求め方を知るといった準場でも問題ないでしょう。
例題
留数定理により積分計算が楽になる例題としては,
- 複素積分($1$位の極における最も基本的な留数の求め方)
- 複素積分($1$位の極における微分を用いた留数の求め方)
- 実積分(有理関数)
- 実積分(被積分関数を簡単に置換すると有理関数に帰着する形)
- 実積分(被積分関数をオイラーの公式で置換すると有理関数に帰着する形)
- 実積分(有理関数と三角関数の組み合わせ)
が挙げられます。それぞれ詳しくみていきましょう。
複素積分($1$位の極における最も基本的な留数の求め方)
次の積分を求めよ。
\oint_{|z|=4}\frac{2z}{(z-1)(z-2)(z-3)}dz
\end{align}
単純閉曲線$|z|=4$内部において被積分関数の$z=1,2,3$は孤立特異点であり,すべて$1$位の極となります。ゆえに,式($\ref{留数_1位の極_基本}$)より
\begin{cases}
\displaystyle
\Res(f(z), 1) = \lim_{z\to 1}(z-1)f(z) = \lim_{z\to 1}\frac{2z}{(z-2)(z-3)} = 1\\[0.7em]
\displaystyle
\Res(f(z), 2) = \lim_{z\to 2}(z-2)f(z) = \lim_{z\to 2}\frac{2z}{(z-1)(z-3)} = -4\\[0.7em]
\displaystyle
\Res(f(z), 3) = \lim_{z\to 3}(z-3)f(z) = \lim_{z\to 3}\frac{2z}{(z-1)(z-2)} = 3\\[0.7em]
\end{cases}
\end{align}
が得られるため,留数定理により
&\oint_{|z|=4}\frac{2z}{(z-1)(z-2)(z-3)}dz\notag\\[0.7em]
&= 2\pi i\left\{\Res(f(z), 1)+\Res(f(z), 2)+\Res(f(z), 3)\right\}
= 0
\end{align}
が得られます。
複素積分($1$位の極における微分を用いた留数の求め方)
次の積分を求めよ。
\oint_{C}\frac{ze^{\pi z}}{z^{4}-16}
\end{align}
ただし,積分路$C$は実軸方向に長さ$1$,虚軸方向に長さ$3$の長方形とする。
$f(z)$は$z=\pm 2,\pm 2i$に$1$位の極をもち,積分路$C$は$z=\pm 2i$のみを含みます。ゆえに,式($\ref{留数_1位の極_微分}$)より
\begin{cases}
\displaystyle
\Res(f(z), 2i) = \lim_{z\to 2i}\frac{ze^{\pi z}}{(z^{4}-16)^{\prime}} = \lim_{z\to 2i}\frac{ze^{\pi z}}{4z^{3}} = \frac{2ie^{2\pi i}}{4(2i)^{3}}=-\frac{1}{16}\\[0.7em]
\displaystyle
\Res(f(z), -2i) = \lim_{z\to -2i}\frac{ze^{\pi z}}{(z^{4}-16)^{\prime}} = \lim_{z\to -2i}\frac{ze^{\pi z}}{4z^{3}} = \frac{-2ie^{-2\pi i}}{4(-2i)^{3}}=-\frac{1}{16}
\end{cases}
\end{align}
が得られるため,留数定理により
\oint_{C}\frac{ze^{\pi z}}{z^{4}-16}
&= 2\pi i\left\{\Res(f(z), 2i)+\Res(f(z), -2i)\right\}
= -\frac{\pi i}{4}
\end{align}
が得られます。
実積分(有理関数)
次の積分を求めよ。
\int_{-\infty}^{\infty}\frac{1}{1+x^{4}}dx
\end{align}
$x$を複素数$z$で置き換えて次の積分経路$C=C_{R}+L_{R}$で複素積分することを考えます。
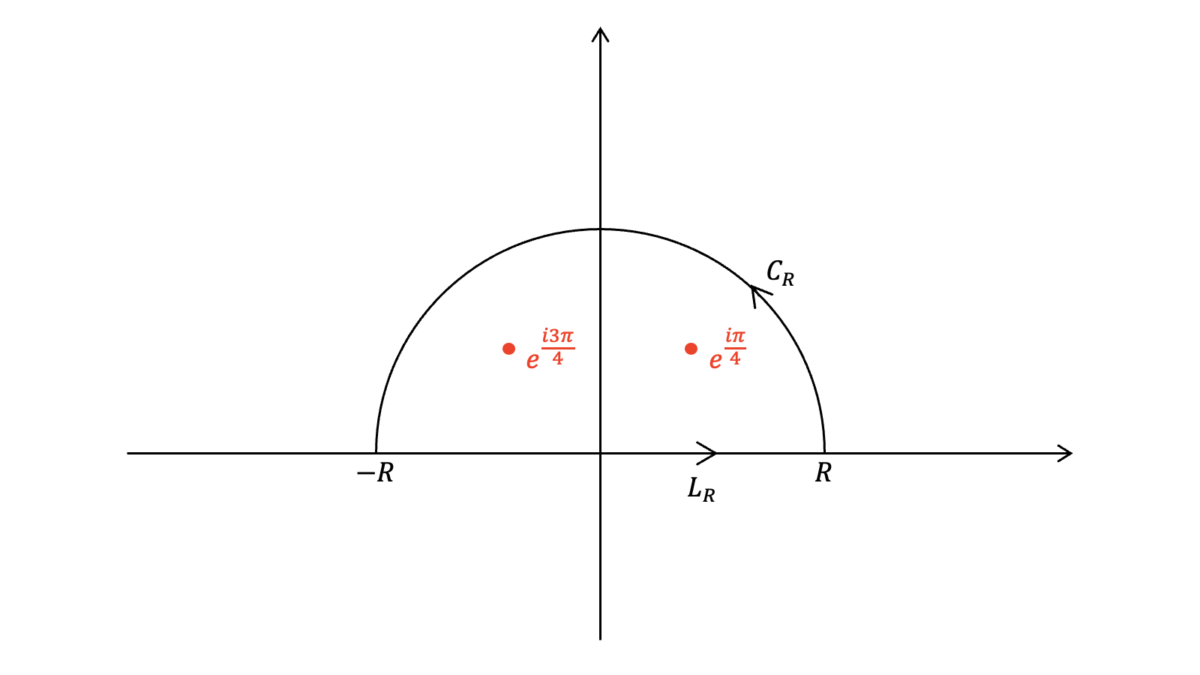
求める積分値は
\lim_{R\to\infty}\int_{L_{R}}\frac{1}{1+z^{4}}dz
&= \lim_{R\to\infty}\int_{C}\frac{1}{1+z^{4}}dz+\lim_{R\to\infty}\int_{L_{R}}\frac{1}{1+z^{4}}dz
\end{align}
となるため,第一項目と第二項目の積分値をそれぞれ求めます。$f(z)$は$z=e^{\pm i\pi/4},e^{\pm i3\pi/4}$に$1$位の極をもち,積分路$C$は$z=e^{i\pi/4},e^{i3\pi/4}$のみを含みます。ゆえに,式($\ref{留数_1位の極_微分}$)より
\begin{cases}
\displaystyle
\Res(f(z), e^{i\pi/4}) = \lim_{z\to e^{i\pi/4}}\frac{1}{(1+z^{4})^{\prime}} = \frac{1}{4e^{i3\pi/4}}=-\frac{1}{2\sqrt{2}(1+i)}=\frac{1-i}{4\sqrt{2}}\\[0.7em]
\displaystyle
\Res(f(z), e^{i3\pi/4}) = \lim_{z\to e^{i3\pi/4}}\frac{1}{(1+z^{4})^{\prime}} = \frac{1}{4e^{i9\pi/4}}=\frac{1}{2\sqrt{2}(-1+i)}=\frac{-1-i}{4\sqrt{2}}
\end{cases}
\end{align}
が得られるため,第一項目について,留数定理を利用すれば
\lim_{R\to\infty}\int_{C}\frac{1}{1+z^{4}}dz
&= 2\pi i\left\{\Res(f(z), e^{i\pi/4})+\Res(f(z), e^{i3\pi/4})\right\}
= \frac{\pi}{\sqrt{2}}
\end{align}
が得られます。第二項目の被極限関数について,三角不等式$|z^{4}+1|\geq |z|^{4}-1$を利用すれば
\left|\int_{L_{R}}\frac{1}{1+z^{4}}dz\right|
&= \int_{L_{R}}\frac{1}{|1+z^{4}|}|dz|\\[0.7em]
&\leq \int_{L_{R}}\frac{1}{|z|^{4}-1}|dz|
= \frac{1}{R^{4}-1}\int_{L_{R}}|dz|\\[0.7em]
&= \frac{\pi R}{R^{4}-1}~\rarr~0~(R\to\infty)
\end{align}
が得られます。以上より,求める答えは
\lim_{R\to\infty}\int_{L_{R}}\frac{1}{1+z^{4}}dz
&= \lim_{R\to\infty}\int_{C}\frac{1}{1+z^{4}}dz+\lim_{R\to\infty}\int_{L_{R}}\frac{1}{1+z^{4}}dz\\[0.7em]
&= \frac{\pi}{\sqrt{2}} + 0 = \frac{\pi}{\sqrt{2}}
\end{align}
となります。
慣れると$L_{R}$上の積分が$0$になることはすぐに分かります。特に数検1級の1次試験では証明の必要はありませんので,頭の中で$L_{R}$上の積分を$0$として$C_{R}$上の積分を留数定理で求めればよいです。
実積分(被積分関数を簡単に置換すると有理関数に帰着する形)
次の積分を求めよ。
\int_{0}^{\pi/2}\sqrt{\tan x}dx
\end{align}
$t=\sqrt{\tan x}$とおくと,
dt = \frac{1}{2\sqrt{\tan x}}\frac{1}{\cos^{2}x}dx = \frac{t^{4}+1}{2t}dx
\end{align}
となるため,与式は
\int_{0}^{\pi/2}\sqrt{\tan x}dx
&= \int_{0}^{\infty}\frac{2t^{2}}{t^{4}+1}
= \int_{-\infty}^{\infty}\frac{t^{2}}{t^{4}+1}
\end{align}
と変形できます。前問の結果を利用すると差分は留数だけであるが,
\begin{cases}
\displaystyle
\Res(f(z), e^{i\pi/4}) = \lim_{z\to e^{i\pi/4}}\frac{z^{2}}{(1+z^{4})^{\prime}} = \frac{e^{i\pi/2}}{4e^{i3\pi/4}}=-\frac{1}{2\sqrt{2}(1+i)}=\frac{1-i}{4\sqrt{2}}\\[0.7em]
\displaystyle
\Res(f(z), e^{i3\pi/4}) = \lim_{z\to e^{i3\pi/4}}\frac{z^{2}}{(1+z^{4})^{\prime}} = \frac{e^{i\pi/2}}{4e^{i9\pi/4}}=\frac{1}{2\sqrt{2}(-1+i)}=\frac{-1-i}{4\sqrt{2}}
\end{cases}
\end{align}
となり留数も一致するため,求める答えは$\displaystyle\frac{\pi}{\sqrt{2}}$となります。
実積分(被積分関数をオイラーの公式で置換すると有理関数に帰着する形)
次の積分を求めよ。
\int_{0}^{2\pi}\frac{1}{5+3\cos\theta}d\theta
\end{align}
$z = e^{i\theta}$とおくと,オイラーの公式より
\cos\theta = \frac{e^{i\theta}+e^{-i\theta}}{2} = \frac{1}{2}\left(z+\frac{1}{z}\right)
\end{align}
となるため,$dz=ie^{i\theta}d\theta=izd\theta$に注意すると,
\oint_{|z|=1}\frac{1}{5+3/2(z+1/z)}\frac{dz}{iz}
&= \frac{2}{i}\oint_{|z|=1}\frac{1}{3z^{2}+10z+3}dz\\[0.7em]
&= \frac{2}{3i}\oint_{|z|=1}\frac{1}{(z+1/3)(z+3)}dz
\end{align}
が得られます。被積分関数を$f(z)$とおくと,$f(z)$は$z=-3,-1/3$に$1$位の極をもち,積分路$C$は$z=-1/3$のみを含みます。ゆえに,式($\ref{留数_1位の極_基本}$)より
\Res(f(z), 2i) = \lim_{z\to -1/3}(z+1/3)\frac{1}{(z+1/3)(z+3)} = \lim_{z\to -1/3}\frac{1}{z+3} = \frac{3}{8}
\end{align}
が得られるため,留数定理により
\frac{2}{3i}\oint_{|z|=1}\frac{1}{(z+1/3)(z+3)}
&= \frac{2}{3i}\cdot 2\pi i\left\{\Res(f(z), -1/3)\right\}
= \frac{4\pi}{3}\cdot\frac{3}{8} = \frac{\pi}{2}
\end{align}
が得られます。
実積分(有理関数と三角関数の組み合わせ)
次の積分を求めよ。
\int_{-\infty}^{\infty}\frac{\cos x}{x^{2}+1}dx
\end{align}
オイラーの公式より
\int_{-\infty}^{\infty}\frac{e^{iz}}{z^{2}+1}dz
= \int_{-\infty}^{\infty}\frac{\cos z}{z^{2}+1}dz+i\int_{-\infty}^{\infty}\frac{\sin z}{z^{2}+1}dz
\end{align}
となるため,与式は
\int_{-\infty}^{\infty}\frac{e^{iz}}{z^{2}+1}dz
\end{align}
の実部を取ることにより得られます。次の積分経路$C=C_{R}+L_{R}$で複素積分することを考えます。
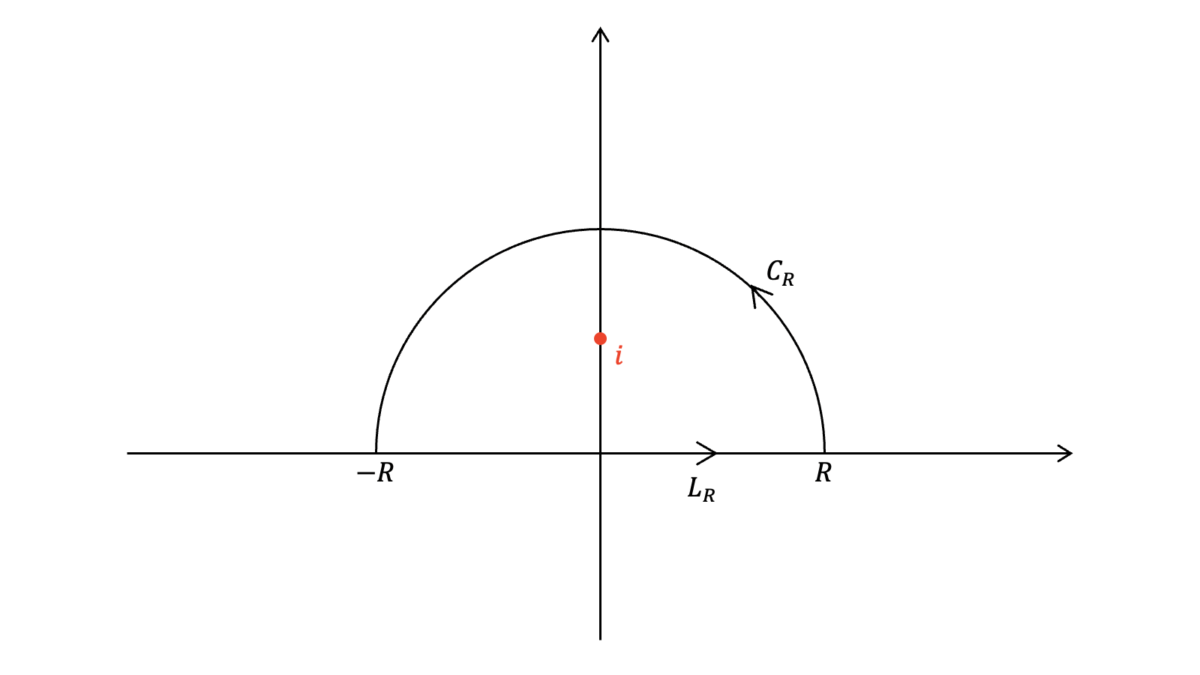
求める積分値は
\lim_{R\to\infty}\int_{L_{R}}\frac{e^{iz}}{z^{2}+1}dz
&= \lim_{R\to\infty}\int_{C}\frac{e^{iz}}{z^{2}+1}dz+\lim_{R\to\infty}\int_{L_{R}}\frac{e^{iz}}{z^{2}+1}dz
\end{align}
となるため,第一項目と第二項目の積分値をそれぞれ求めます。$f(z)$は$z=\pm i$に$1$位の極をもち,積分路$C$は$z=i$のみを含みます。ゆえに,式($\ref{留数_1位の極_微分}$)より
\Res(f(z), i) = \lim_{z\to i}\frac{e^{iz}}{(1+z^{2})^{\prime}} = \frac{e^{-1}}{2i}
\end{align}
が得られるため,第一項目について,留数定理を利用すれば
\lim_{R\to\infty}\int_{C}\frac{e^{iz}}{z^{2}+1}dz
&= 2\pi i\Res(f(z), i)
= \frac{\pi}{e}
\end{align}
が得られます。第二項目の被極限関数について,三角不等式$|z^{2}+1|\geq |z|^{2}-1$と
|e^{iz}|=|e^{i(x+yi)}|=|e^{ix}|\cdot|e^{-y}|=|e^{-y}|\geq 1
\end{align}
を利用すれば
\left|\int_{L_{R}}\frac{e^{iz}}{z^{2}+1}dz\right|
&= \int_{L_{R}}\frac{e^{iz}}{|z^{2}+1|}|dz|\\[0.7em]
&\leq \int_{L_{R}}\frac{1}{|z|^{2}-1}|dz|
= \frac{1}{R^{2}-1}\int_{L_{R}}|dz|\\[0.7em]
&= \frac{\pi R}{R^{2}-1}~\rarr~0~(R\to\infty)
\end{align}
が得られます。以上より,
\lim_{R\to\infty}\int_{L_{R}}\frac{1}{1+z^{4}}dz
&= \lim_{R\to\infty}\int_{C}\frac{1}{1+z^{4}}dz+\lim_{R\to\infty}\int_{L_{R}}\frac{1}{1+z^{4}}dz\\[0.7em]
&=\frac{\pi}{e} + 0 = \frac{\pi}{e}
\end{align}
となるため,そのまま実部を取ることにより求める答えは$\displaystyle\frac{\pi}{e}$となります。


コメント