本記事は数学の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
目次
主要な関数のオーダ比較
主要な関数のオーダの大小関係は,以下のように表される。
\begin{align}
a \prec \log n \prec n \prec n\log n \prec n^{a} \prec a^{n} \prec n! \prec n^{n}
\label{主題}
\end{align}
a \prec \log n \prec n \prec n\log n \prec n^{a} \prec a^{n} \prec n! \prec n^{n}
\label{主題}
\end{align}
ただし,$\prec$は関数の漸近的な増加の勢いに関する大小関係を表し,$a>2$は定数,$n$は変数を表す。
オーダーの大小関係は,漸近的な増加の勢いを評価していることに注意して下さい。
証明
一番左の$\prec$から一番右の$\prec$までを①から⑦にナンバリングして,それぞれを「オーダーの大小関係の定義」から証明します。全てに共通して,オーダーの大きい方を分母で小さい方を分子とした分数関数の極限を考えたときに$0$に収束することを示します。
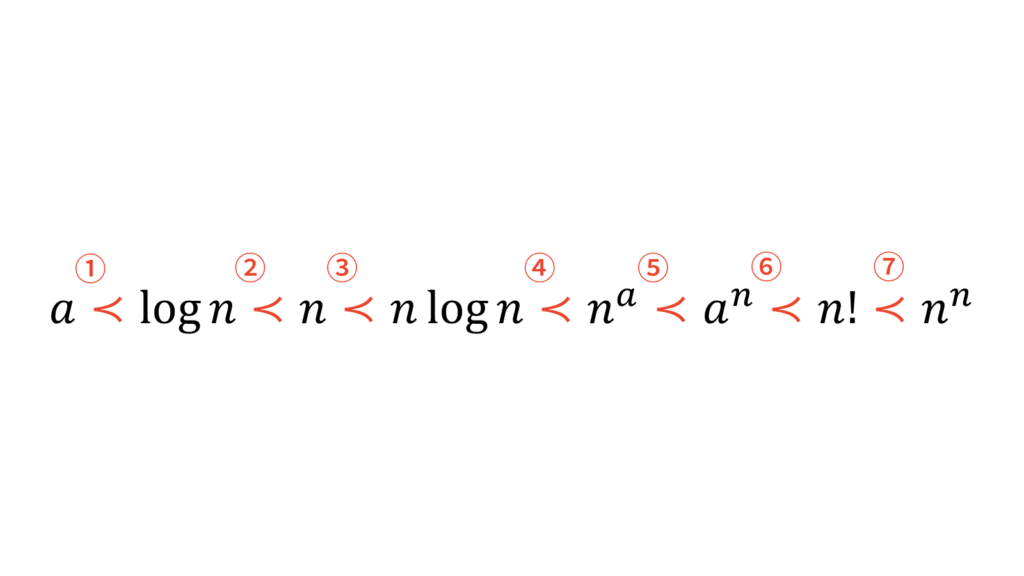
①の証明
自明とすることが多いです。
\begin{align}
\lim_{n\rightarrow \infty} \left| \frac{a}{\log n} \right| &= 0
\end{align}
\lim_{n\rightarrow \infty} \left| \frac{a}{\log n} \right| &= 0
\end{align}
②の証明
ロピタルの定理を利用します。
\begin{align}
\lim_{n\rightarrow \infty} \left| \frac{\log n}{n} \right| &= \lim_{n\rightarrow \infty} \left| \frac{1}{n} \right| \\[0.7em]
&= 0
\end{align}
\lim_{n\rightarrow \infty} \left| \frac{\log n}{n} \right| &= \lim_{n\rightarrow \infty} \left| \frac{1}{n} \right| \\[0.7em]
&= 0
\end{align}
③の証明
自明とすることが多いです。
\begin{align}
\lim_{n\rightarrow \infty} \left| \frac{n}{n\log n} \right| &= \lim_{n\rightarrow \infty} \left| \frac{1}{\log n} \right| \\[0.7em]
&= 0
\end{align}
\lim_{n\rightarrow \infty} \left| \frac{n}{n\log n} \right| &= \lim_{n\rightarrow \infty} \left| \frac{1}{\log n} \right| \\[0.7em]
&= 0
\end{align}
④の証明
ロピタルの定理を利用します。
\begin{align}
\lim_{n\rightarrow \infty} \left| \frac{n\log n}{n^{a}} \right| &= \lim_{n\rightarrow \infty} \left| \frac{\log n}{n^{a-1}} \right| \\[0.7em]
&= \lim_{n\rightarrow \infty} \left| \frac{1}{(a-1)n^{a-1}} \right| \\[0.7em]
&= 0
\end{align}
\lim_{n\rightarrow \infty} \left| \frac{n\log n}{n^{a}} \right| &= \lim_{n\rightarrow \infty} \left| \frac{\log n}{n^{a-1}} \right| \\[0.7em]
&= \lim_{n\rightarrow \infty} \left| \frac{1}{(a-1)n^{a-1}} \right| \\[0.7em]
&= 0
\end{align}
⑤の証明
ロピタルの定理を$n$回適用します。
\begin{align}
\lim_{n\rightarrow \infty} \left| \frac{n^{a}}{a^{n}} \right| &= \lim_{n\rightarrow \infty} \left| \frac{a!}{(\log a)^n a^{n}} \right| \\[0.7em]
&= 0
\end{align}
\lim_{n\rightarrow \infty} \left| \frac{n^{a}}{a^{n}} \right| &= \lim_{n\rightarrow \infty} \left| \frac{a!}{(\log a)^n a^{n}} \right| \\[0.7em]
&= 0
\end{align}
⑥の証明
$a$より大きな整数のうち一番小さな整数を$b$と置くと,以下が得られます。
\begin{align}
\lim_{n\rightarrow \infty} \left| \frac{a^{n}}{n!} \right| &<
\lim_{n\rightarrow \infty} \left| \left(\frac{a}{b}\right)^{n-a}\frac{a}{a}\frac{a}{a-1}\cdots \frac{a}{1} \right| \\[0.7em]
&= 0
\end{align}
\lim_{n\rightarrow \infty} \left| \frac{a^{n}}{n!} \right| &<
\lim_{n\rightarrow \infty} \left| \left(\frac{a}{b}\right)^{n-a}\frac{a}{a}\frac{a}{a-1}\cdots \frac{a}{1} \right| \\[0.7em]
&= 0
\end{align}
したがって,はさみうちの原理より以下が示されます。
\begin{align}
\lim_{n\rightarrow \infty} \left| \frac{a^{n}}{n!} \right| &= 0
\end{align}
\lim_{n\rightarrow \infty} \left| \frac{a^{n}}{n!} \right| &= 0
\end{align}
⑦の証明
自明とすることが多いです。
\begin{align}
\lim_{n\rightarrow \infty} \left| \frac{n!}{n^{n}} \right| &= \lim_{n\rightarrow \infty} \left| \frac{n}{n}\frac{n-1}{n}\cdots \frac{1}{n} \right| \\[0.7em]
&= 0
\end{align}
\lim_{n\rightarrow \infty} \left| \frac{n!}{n^{n}} \right| &= \lim_{n\rightarrow \infty} \left| \frac{n}{n}\frac{n-1}{n}\cdots \frac{1}{n} \right| \\[0.7em]
&= 0
\end{align}


コメント