本記事は機械学習の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
はじめに
本章では,基礎スキーの概要を述べた後に,IDEF0と部分的最小二乗法に関する簡単な説明を行います。
基礎スキーとは
基礎スキーは,審判により設定された雪面において,落下速度や回転の鋭さ,身体運動の美しさを競う採点競技です。旗門によって制限された雪面を滑走する速度を競うアルペン競技とは異なり,基礎スキーでは用具の進化などに伴って変化する合理性を追求するスポーツです。
例えば,数十年前に到来したスキーバブルの時代では,多くの選手は2メートルにも及ぶ長さのスキー板を扱っており,オーストリアのバインシュピール技術を拡張したウェーデルンと呼ばれる滑降技術が取り入れられました。最近では,カービングスキーが開発された影響から,ウェーデルンのような雪面を削る動作を含む身体運動を行うことはせず,極力減速要素の少ない滑降技術が積極的に用いられるようになっています。
基礎スキーには二面性が存在します。すなわち,競技として勝敗を競うことが目的の場合と,美しく滑れるようになることが目的の場合がある。前者の場合は点数という客観的な指標に基づいて滑りが評価され,後者の場合は自己満足度という主観的な指標に基づいて滑りが評価されます。両者には,競技であるか否かという違いがある一方で,スキー技術を向上させたいという動機に関して明確な共通点があります。
本記事は,基礎スキーに打ち込む管理人の技術向上を目指すため,上達機構をモデル化することで,今後の練習指針を定めるものです。ここでは,基礎スキーの二面性に着目して,基礎スキーにおける上達の定義を採点結果の向上(客観上達)と自己満足度の向上(主観上達)に細分化して上達機構のモデル化を行うものとします。具体的には,客観・主観上達機構の把握と分析を行うため,integrated definition methodology (IDEF)のうちIDEF0を用います。さらに,効果的な練習指針を解析するため,全日本予選会の動画データから得られた統計量に対して部分的最小二乗法を用います。
IDEF0とは
IDEF0に関するコラムは,以下の拙記事をご覧ください。

IDEF0は,複雑な対象(Function/Activity)を複数人で合意しながら分析することを可能にします。汎用的な図式表現であることから,必ずしも複数人で用いる手法ではなく,個人の活動に適用することもできます。
IDEF0は,A-0上位層と下位層から構成されます。
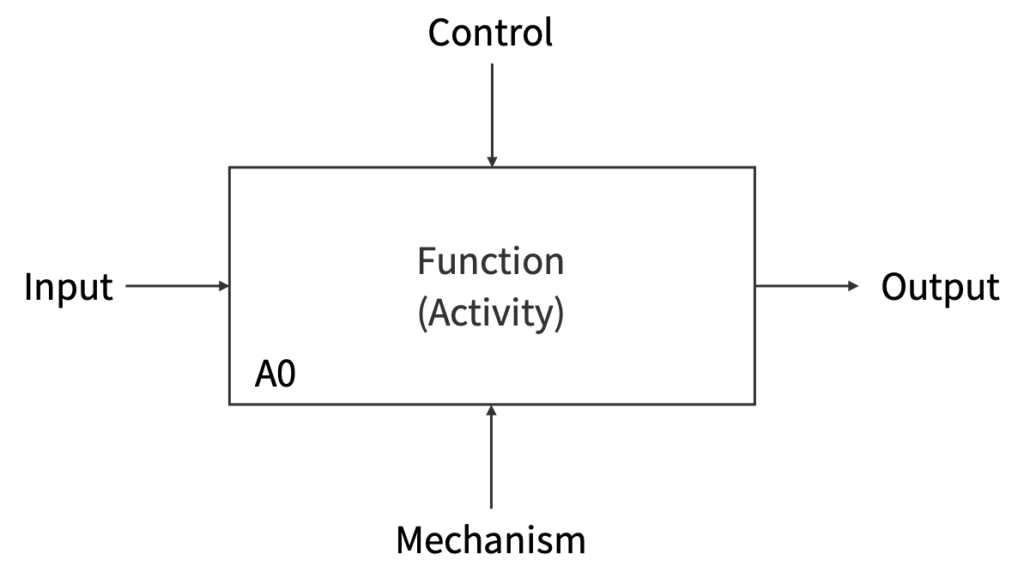
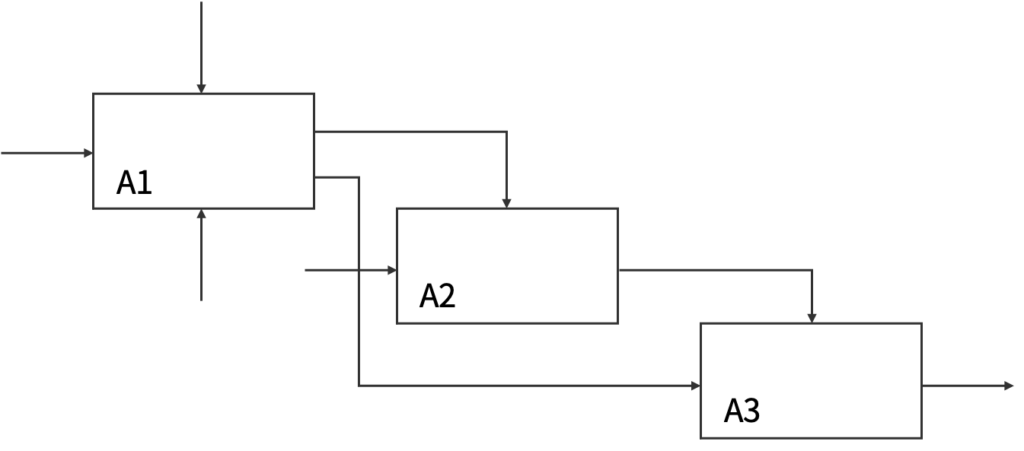
A-0上位層では目的と観点を記述し,下位層ではA-0をより詳細に記述します。Inputは解析対象の入力,Controlは制約,Mechanismは支援機構,Outputは出力を表します。Function(Activity)には動詞が入ることに注意されたいです。
本記事では,基礎スキーにおける上達の定義を客観上達と主観上達に細分化することに注意して,2つの目的に対してA-0上位層を作成したうえで,それぞれに対して下位層を作成することにします。
なお,観点としては25歳スキー歴5年男性を採用します。
部分的最小二乗法
最小二乗法の詳しい説明は,以下の拙記事をご覧ください。

部分的最小二乗法は,線形回帰分析を行うための手法の1つです。一般に,線形回帰では説明変数に相関がある場合に多重共線性が生じること,サンプル数が極端に少ない場合にモデルが一意に定まらないこと,データ含まれるノイズに大きな影響を受けることなどの問題が生じてしまいます。
そこで,部分的最小二乗法では,全てのデータを踏まえて生成された無相関な新しい説明変数(潜在変数)を用い,重要度(標準回帰係数)の高い潜在変数から順番に用いることで上述の問題を解決しようとします。
本記事では,基礎スキーにおける小回り種目に焦点を当てて,2019年度近畿スキー技術選手権大会兼全日本スキー技術選手権大会予選会の動画から収集されたデータに対して部分的最小二乗法を適用します。具体的には,設定された斜面を滑り切るためのターン数[回]と滑走時間[s],全体を通したダイナミック度,左右差,ミス数[回],そしてその滑りに付けられた点数[point]を集計します。
なお,ダイナミック度と左右差は管理人が独断的に付与した$[0,1]$の値です。説明変数はターン数,滑走時間,ダイナミック度,左右差,ミス数の5つであり,目的変数は点数です。このデータを通して,客観上達に関する解析を行なっていきます。
実験結果
本章では,IDEF0に関する実験結果と部分的最小二乗法に関する実験結果を述べます。
IDEF0
以下の図は,それぞれ客観上達に関してのA-0上位層,下位層を表します。ここで,主観上達のIDEF0に関しては,図中赤色の部分「目標点数」を「好み」に変更すればよいです。
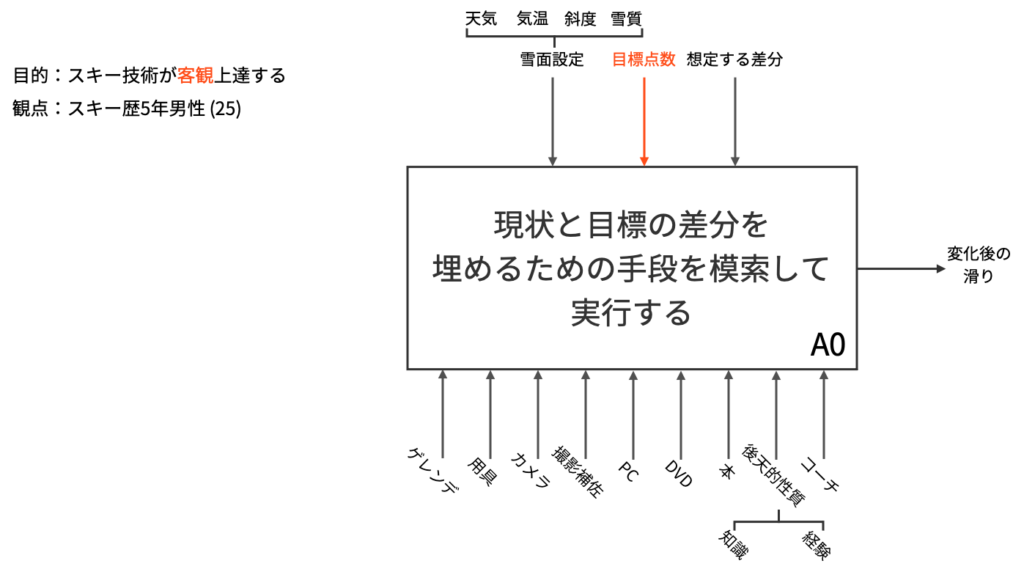
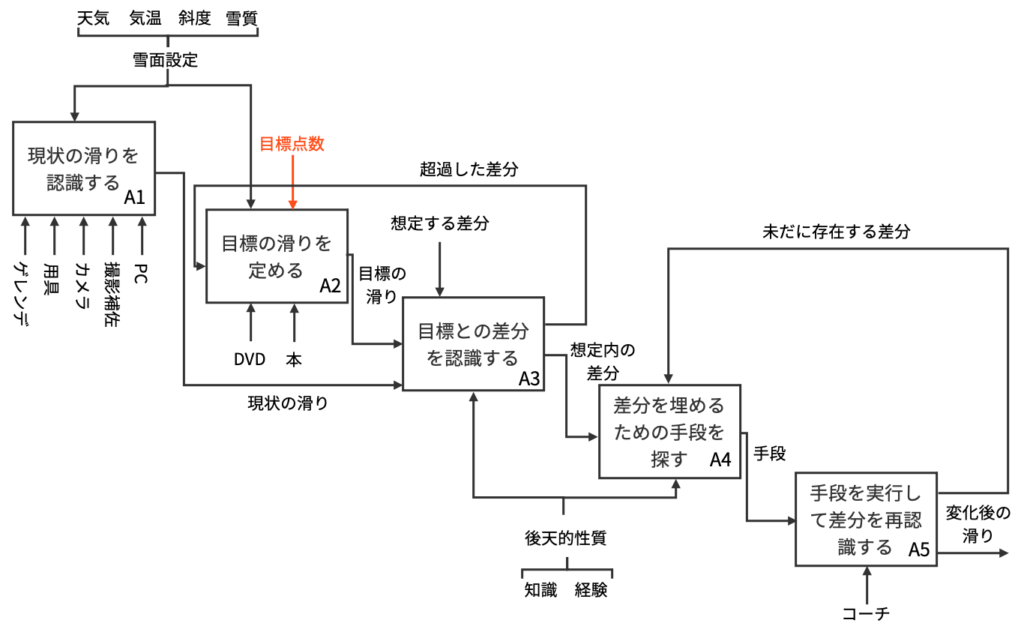
示したIDEF0について補足説明を行います。主観客観問わず,スキーが上達するためには目標との差分を埋め合わせる必要があります。逆に言えば,目標へと少しでも近づいた場合に基礎スキーヤーは上達したと見なされるのです。そのために,まずは現状の滑りを認識する必要があります。目標を定める際には,先輩の動画や有名選手の滑りが映っているDVD,技術解説がなされている書籍等を参考にするとよいです。
しかし,目標があまりにも高すぎる場合は差分を埋めることが難しいため,あらかじめ差分を想定しておく必要があります。目標との差分を認識した際に,想定との差分から超過してしまった場合には,目標の滑りを定め直す必要があります。現状の滑りの認識と目標の滑りを決定する際には,天気や気温,斜度,雪質に代表されるような雪面設定を仮定する必要があります。例えば,コブ斜面と整地では滑り方が異なるために,現状の滑りや目標の滑りもそれに応じて定まることになります。
目標が定まり次第,目標との差分を埋めるために,然るべき手段を見つけ出す必要があります。差分を認識して手段を探すという行為には,知識や経験という後天的性質が必要となる場合が多いです。なぜなら,目標と現状の滑りを比較した際に,至らない箇所を言語化するためには知識が必要であり,それを雪面設定に応じて行うためには十分な経験が必要だからです。
さらに,差分を認識したところで,どのような典型的アプローチが取られているかどうかという知識がないことには,差分を埋めるための手段を探すことは難しいです。手段が見つかった後は,実際にその手段を実行して差分を再認識することになります。手段を実行した後にも差分が未だ存在する場合は,差分を埋めるための手段を再び探す必要があります。
上記議論が主観上達に切り替えられた場合でも,目標を定める際のControlが「好み」に置き換えるだけで同様の議論が可能です。
部分的最小二乗法
収集したデータを以下の表に示します。
| ターン数 | 滑走時間 | ミス | 左右差 | ダイナミック度 | 点数 |
|---|---|---|---|---|---|
| 16 | 10.83 | 0 | 0.3 | 0.1 | 248 |
| 12 | 7.93 | 0 | 0.1 | 0.7 | 258 |
| 11 | 7.23 | 0 | 0.2 | 0.8 | 256 |
| 13 | 8.15 | 0 | 0.3 | 0.2 | 252 |
| 16 | 9.47 | 0 | 0.1 | 0.5 | 259 |
| 13 | 8.60 | 1 | 0.3 | 0.6 | 255 |
| 18 | 12.3 | 0 | 0.2 | 0.1 | 248 |
| 14 | 9.25 | 2 | 0.2 | 0.4 | 245 |
| 15 | 9.85 | 1 | 0.5 | 0.9 | 256 |
| 15 | 9.39 | 0 | 0.2 | 0.6 | 254 |
| 14 | 11.69 | 0 | 0.1 | 0.1 | 231 |
| 10 | 6.90 | 0 | 0.2 | 0.9 | 255 |
| 14 | 9.15 | 0 | 0.1 | 0.7 | 255 |
| 15 | 9.73 | 0 | 0.3 | 0.5 | 253 |
| 13 | 8.45 | 0 | 0.3 | 0.7 | 256 |
| 15 | 10.03 | 0 | 0.1 | 0.7 | 264 |
indexは1から始まり,点数は297点満点です。実際に部分的最小二乗法を適用する際には,全ての説明変数と目的変数を最小値0,最大値1になるように正規化を行ないました。部分的最小二乗法の次元数を決定するため,4-交差分割検証を行ないました。その結果を以下の表に示します。
| $k$ | $r=1$ | $r=2$ | $r=3$ | $r=4$ | $r=5$ |
|---|---|---|---|---|---|
| 1 | 0.81 | 0.48 | 0.75 | 3.54 | 3.54 |
| 2 | 0.35 | 0.65 | 0.65 | 0.66 | 0.64 |
| 3 | 1.15 | 2.25 | 3.27 | 3.89 | 2.01 |
| 4 | 1.25 | 0.70 | 0.59 | 0.69 | 0.66 |
| PRESS | 3.56 | 4.08 | 5.26 | 8.77 | 7.07 |
この結果から,閾値1のWold’s R criterionに従えば,交差分割検証における予測残差平方和の和(PRESS)が局所的に最小値をとる次元数を採用するため,次元数は1にすればよいことが分かります。次元数を1に設定して部分的最小二乗法を施したときの(累積)寄与率と説明変数に対する重み行列(今回は次元が1のためベクトル)の要素を以下の表に示します。
| 説明変数 | 説明変数 | 目的変数 | 目的変数 | |
|---|---|---|---|---|
| 潜在変数 | 寄与率 | 累積寄与率 | 寄与率 | 累積寄与率 |
| 1 | 0.73 | 0.73 | 0.89 | 0.89 |
| 2 | 0.14 | 0.87 | 0.05 | 0.94 |
| 3 | 0.08 | 0.95 | 0.01 | 0.95 |
| 4 | 0.01 | 0.96 | 0.02 | 0.97 |
| 5 | 0.04 | 1.00 | 0.00 | 0.97 |
| ターン数 | 滑走時間 | ミス数 | 左右差 | ダイナミック度 |
|---|---|---|---|---|
| 0.52 | 0.43 | 0.12 | 0.32 | 0.66 |
実装
まずデータをベタ打ちします。csvではないので苦肉の策。
import numpy as np
data = np.array(
[[16 , 10.83 , 0 , 0.3 , 0.1 , 248],
[12 , 7.93 , 0 , 0.1 , 0.7 , 258],
[11 , 7.23 , 0 , 0.2 , 0.8 , 256],
[13 , 8.15 , 0 , 0.3 , 0.2 , 252],
[16 , 9.47 , 0 , 0.1 , 0.5 , 259],
[13 , 8.60 , 1 , 0.3 , 0.6 , 255],
[18 , 12.3 , 0 , 0.2 , 0.1 , 248],
[14 , 9.25 , 2 , 0.2 , 0.4 , 245],
[15 , 9.85 , 1 , 0.5 , 0.9 , 256],
[15 , 9.39 , 0 , 0.2 , 0.6 , 254],
[14 , 11.69 , 0 , 0.1 , 0.1 , 231],
[10 , 6.90 , 0 , 0.2 , 0.9 , 255],
[14 , 9.15 , 0 , 0.1 , 0.7 , 255],
[15 , 9.73 , 0 , 0.3 , 0.5 , 253],
[13 , 8.45 , 0 , 0.3 , 0.7 , 256],
[15 , 10.03 , 0 , 0.1 , 0.7 , 264]])続いてデータの正規化を行います。
# データのインデックスをバラバラにするための数列
x_rand = np.random.permutation(data.shape[0])
# 並び替え実行
data = data[x_rand, :]
# 説明変数
X = data[:, :5]
# 目的変数
y = data[:, -1]
# 正規化
X_norm = (X-np.min(X, axis=0)) / np.max(X-np.min(X, axis=0), axis=0)
y_norm = (y-np.min(y, axis=0)) / np.max(y-np.min(y, axis=0), axis=0)交差検証で潜在変数の次元数を決定します。以下のコードでは,潜在変数の次元数を1〜5まで手動で変えていく必要があります。
# 潜在変数の次元数
n_r = 6
# 交差分割の分割数
n_fold = 4
# 予測平方和のリスト
E_list = []
# 交差分割開始
for n_split in range(n_fold):
print(f"{n_split+1}fold目開始")
# 交差分割のtrain, testのインデックスペアを求める
index_train = np.arange(n_split*4, (n_split + 1)*4)
index_test = np.array([i for i in range(data.shape[0]) if i not in index_train])
# trainデータとtestデータの取り出し
X_train = X_norm[index_train, :]
y_train = y_norm[index_train]
X_test = X_norm[index_test, :]
y_test = y_norm[index_test]
# 寄与率のための計算
X_test_sum = np.sum(X_test**2)
y_test_sum = np.sum(y_test**2)
# testで使うための入れ物
w_list = []
z_list = []
s_list = []
t_list = []
CX_list = []
Cy_list = []
# 重要な次元から繰り返し更新していく
print(f"---train---")
for r in range(n_r):
# w, z, s, tの計算
w = (X_train.T @ y_train) / np.linalg.norm(X_train.T @ y_train)
z = X_train @ w
s = (X_train.T @ z) / (z.T @ z)
t = (y_train.T @ z) / (z.T @ z)
zs = z[:,None] @ s[:,None].T
zt = z * t
# デフレーション
X_train -= zs
y_train -= zt
# 保存
w_list.append(w)
z_list.append(z)
s_list.append(s)
t_list.append(t)
# test開始
print(f"---test---")
E_list_comp = []
for r in range(n_r):
# train時のw, s, tを利用
w = w_list[r]
z = X_test @ w
s = s_list[r]
t = t_list[r]
zs = z[:,None] @ s[:,None].T
zt = z * t
# 寄与率のための計算
CX_list.append(np.sum(X_test**2) - np.sum((X_test - zs)**2))
Cy_list.append(np.sum(y_test**2) - np.sum((y_test - zt)**2))
X_test -= zs
y_test -= zt
E = np.sum(y_test**2)
E_list.append(E)
# 予測平方和の表示
print(E_list)
print(sum(E_list))
# 累積寄与率の表示
print(np.round((CX_list / X_test_sum) * 100, 2))
print(np.round((Cy_list / y_test_sum) * 100, 2))さて,全てのデータに対して潜在変数の次元数を1にして部分的最小二乗法適用します。先ほどのコードとほとんど同じです。
X = data[:, :5]
y = data[:, -1]
X_norm = (X-np.min(X, axis=0)) / np.max(X-np.min(X, axis=0), axis=0)
y_norm = (y-np.min(y, axis=0)) / np.max(y-np.min(y, axis=0), axis=0)
n_r = 1
X_norm_sum = np.sum(X_norm**2)
y_norm_sum = np.sum(y_norm**2)
z_list = []
s_list = []
t_list = []
CX_list = []
Cy_list = []
for r in range(n_r):
w = (X_norm.T @ y_norm) / np.linalg.norm(X_norm.T @ y_norm)
z = X_norm @ w
s = (X_norm.T @ z) / (z.T @ z)
t = (y_norm.T @ z) / (z.T @ z)
zs = z[:,None] @ s[:,None].T
zt = z * t
CX_list.append(np.sum(X_norm**2) - np.sum((X_norm - zs)**2))
Cy_list.append(np.sum(y_norm**2) - np.sum((y_norm - zt)**2))
X_norm -= zs
y_norm -= zt
z_list.append(z)
s_list.append(s)
t_list.append(t)
# 累積寄与率の表示
print(np.round((CX_list / X_norm_sum) , 2))
print(np.round((Cy_list / y_norm_sum) , 2))考察
本章では,IDEF0に関する考察と部分的最小二乗法に関する考察を述べます。
IDEF0
客観上達と主観上達のIDEF0を作成することで,両者の違いを生み出しているのはA2において目標の滑りを定める際のControlだということが分かりました。このことから,主観上達というのも結局は客観的な事象であるという仮説が考えられます。客観上達における「目標点数」が第三者によるジャッジにおいて付与される評価値であるのに対し,主観上達における「好み」もゲレンデで第三者に見せつけたいといったような自己顕示欲や好きなスキーヤーに一歩でも近づきたいといったような憧憬に基づいて評価されるものです。したがって,本稿で行なった客観上達・主観上達という区分け自体が重要なのではなく,スキー技術を向上させたいといった場合には客観的な評価指標が必ず介在することを理解できました。
第三者の協力がなければスキー技術の向上は難しいです。例えば,A1におけるMechanismの撮影補助やA5におけるMechanismのコーチが第三者の協力に該当します。特に,コーチに関しては客観上達と主観上達で果たすべき役割が変わります。客観上達においては,点数を出すことが何よりも優先され,自分の気持ちや憧れの優先度は限りなく低くなります。一方で,主観上達においては,コーチは受講生に対しヒアリングを行う必要があり,必ず対話的にA3で認識された目標との差分を埋める作業を行う必要があります。現状,基礎スキー界のコーチには,客観上達と主観上達を混同している人が多く,受講生のニーズとマッチしないケースが多く見られます。
基礎スキーの特性として,足の速さや背の高さといった先天的な特質に依存する部分が少ないことが指摘できます。サッカーやバスケットボールのようなスポーツでは,本記事で示したようなIDEF0に従って上達モデルを組んだとしても,先天的な特質の違いによって目標との差分が埋められない場合があります。一方で,基礎スキーというスポーツでは,有利にはたらく先天的な特質が非常に少なく,A4において適切なアプローチを選択できれば,努力が反映されやすい傾向にあります。
本記事で作成したIDEF0の想定する期間は1週間程度です。スキーはシーズンスポーツであるため,年間を通じたコーディネーションが必要になります。「現状の滑り」はシーズンを終えてから次のシーズンに入るまでに変わってしまう可能性が非常に高いため,頻繁にA1を行うことが望ましいと考えられます。同時に,シーズンごとに用具や流行りの滑りが変化するため,A2も頻繁に行うことが望ましいです。スキーは天気に代表されるような環境要因に左右されやすいスポーツです。雪山では吹雪や雨など過酷な状況下での練習を強いられる場合があるため,A1に用いるカメラにはできる限り性能の高いものを利用するべきです。例えば,防水性能が付いていなければ,吹雪や雨の場合にA1を行うことが不可能になってしまいます。また,長距離撮影ができないカメラを利用してしまうと,距離の長いゲレンデにおいてA1を行うことが難しくなってしまいます。
以上の考察から,効果的な練習方針の要素として,頻繁にA1とA2を行うこと,その際にはできる限り性能の高いカメラを利用すること,そして第三者と滑る機会を積極的に作ることなどが挙げられます。
部分的最小二乗法
先ほどの表から,次元数が増えるにしたがって 過学習を起こす傾向が見られることが分かります。 閾値1のWold’s R criterionに従えば $r=1$が採用されますが, $k=4$では 他のどの次元数よりも予測残差平方和が最大となってしまっているため,必ずしも$r=1$が最適な次元数とは限らないと考えられます。例えば,データを他の大会からも収集して分割数をより大きくしたうえで, 予測残差平方和の分散などを考慮して次元数を決めることができれば,より頑健なモデルを構築することが可能になると考えられます。
先ほどの表から,十分な累積寄与率を0.9とすると,潜在変数の次元数が1の場合でも目的変数は十分表現できていることが分かります。 一方で,説明変数をよく表現するためには,次元数を3に設定する必要があります。
先ほどの表は,潜在変数における説明変数それぞれの係数を表します。すなわち,これらの係数は 説明変数の各要素がどれだけ潜在変数に利用されているかを表す値です。この結果をみると,目的変数である点数をよく表現するためには ダイナミック度が重要な指標である一方で,ミスは相対的に重要な指標ではないことが分かります。しかし,実際の採点現場では,1回でもミスをすると大きく減点されてしまうため,ミスは非常に重要な指標です。今回収集したデータには,ダイナミック度が高いがミスをしてしまうことで 点数が大きく下がってしまうという例がなく,ほとんどの選手がミスをしていなかったことから,ミスの回数は重要な指標ではないと モデルが判断したものと考えられます。
実験結果から推測される効果的な練習方法の方針は,ダイナミック度を向上させるということです。しかし,現実的には ターン数や滑走時間も重要な要素であることが考えられるため,より多くのデータを収集したうえで,説明変数の項目を検討し直し,適切な次元数を選んで 再び部分的最小二乗法を用いて解析を行う必要があると考えられます。


コメント