本記事では，数学検定1級で頻出のトピックについてまとめていきます。
初学者の分かりやすさを優先するため，多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
複素数の絶対値とアポロニウスの円
$2$点$A,B$からの距離の比が$m:n$で一定となる点の軌跡は円となり，これをアポロニウスの円という。アポロニウスの円は複素平面上でも定義され，複素数$\alpha,\beta$に対して
n|z-\alpha| = m|z-\beta|
\end{align}
を満たす$z$の軌跡として表される。
アポロニウスの円に関連した問題では，$2$点$A,B$を結んだ直線上に問題を解くためのヒントが隠されていることが多い。例えば，$AB$を内分する点と外分する点が円の両端となるため，その長さを$1/2$をすれば半径が得られる。複素数の絶対値の等式は，アポロニウスの円を利用することが解くことができるケースが多い。
以下の例題を見ることで具体的にイメージが湧くはずです。
例題
$|z|=1$の下で，
|iz+2|=|cz+1|
\end{align}
を満たす複素数$c$を求めよ
両辺とも$z$からの距離を表しているため，この等式はアポロニウスの円を表しています。左辺の始点は左辺が$0$となる点であるため$-2i$となり，同様に右辺の始点は$-1/c$となるため，この問題では$-2i$と$-1/c$からの距離が単位円となるような$c$を求めればよいことが分かります。
対称性から$-1/c$は虚軸上に存在します。$-2i$と$-1/c$の内分点が$-i$であることから$-1/c$は負の領域に存在します。$|c|=c^{\prime}$とおくと，下図のようになります。
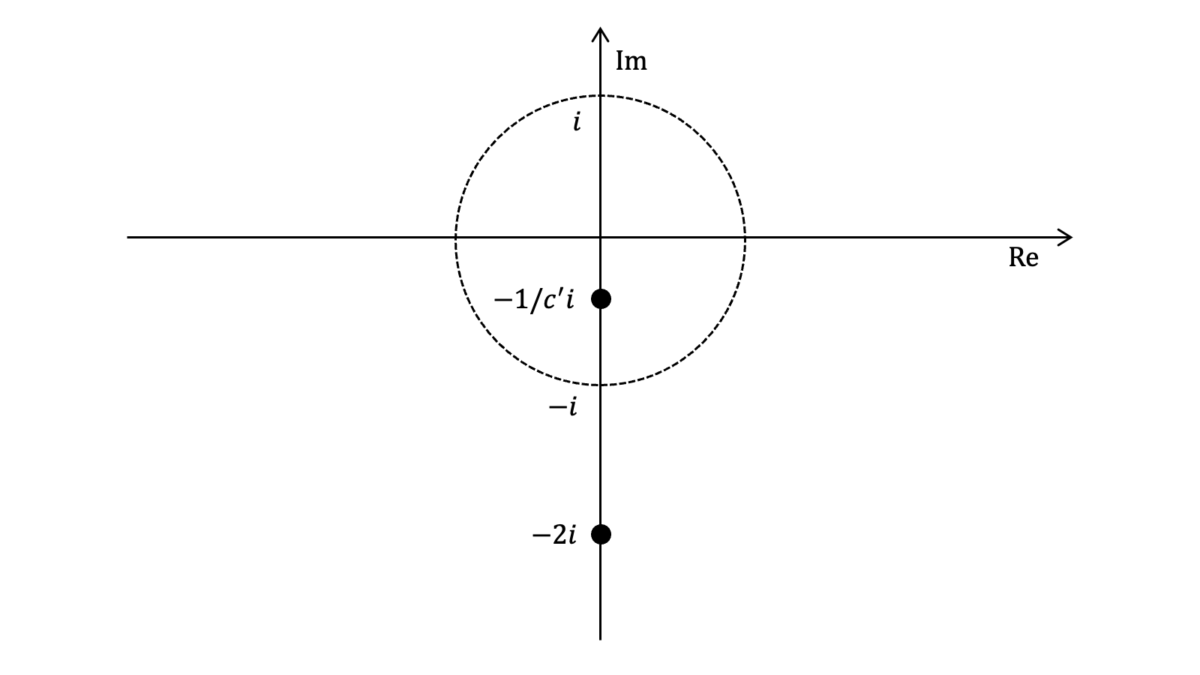
内分の比と外分の比が等しくなることから，
\left(1-\frac{1}{c^{\prime}}\right):1=\left(1+\frac{1}{c^{\prime}}\right):3
\end{align}
となるため，$c^{\prime}=2$が得られます。したがって，求める答えは$c=-2i$です。
一般化
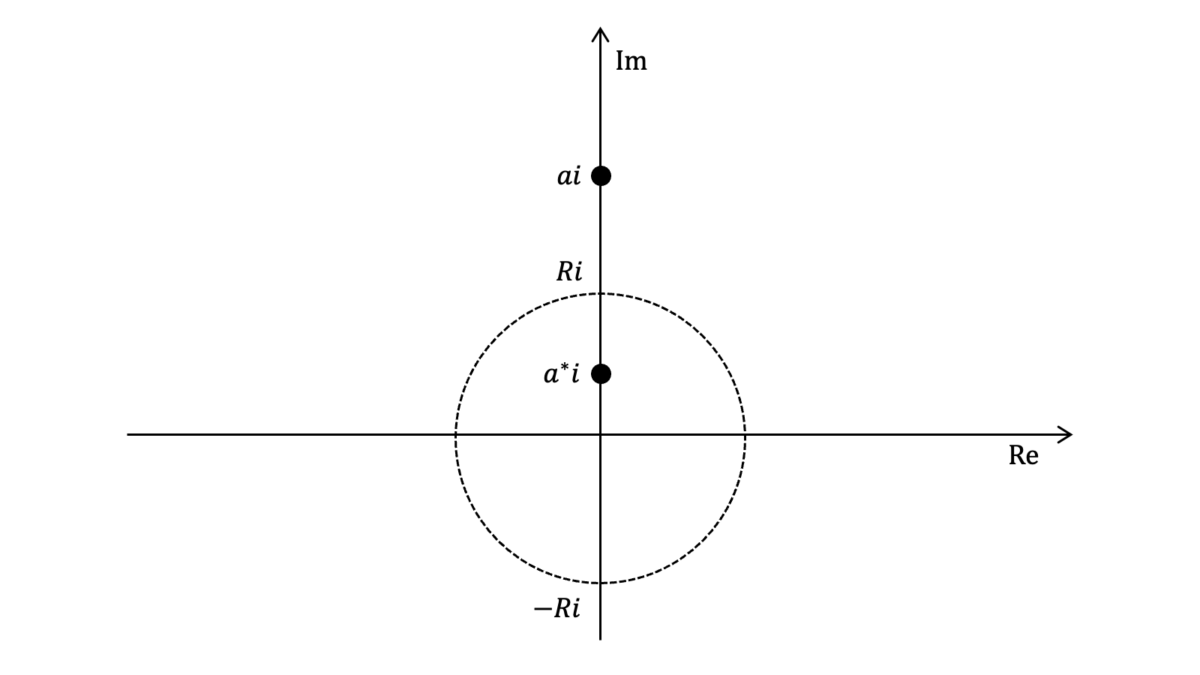
実数$a>0$に対し，$ai$と$a^{\ast}i$からの距離が等しいアポロニウスの円が，原点を中心とする半径$R$の円になったとします。このとき，上と同様に内分の比と外分の比が等しくなることから
(R-a^{\ast}):(a-R)=(R+a^{\ast}):(a+R)
\end{align}
となるため，
a^{\ast}=\frac{R^{2}}{a}
\end{align}
が得られます。
この関係を複素数を用いて表します。すなわち，ある複素数$c$に対し，アポロニウスの円が原点が$0$で半径$R$の円となるようなもう片方の点は，
- 長さは$R^{2}/|c|$
- 偏角は変わらない
を満たすような複素数$c^{\ast}$となります。この$c^{\ast}$を$c$を用いて表しましょう。長さが$R^{2}/|c|$となる複素数は$R^{2}/c$ですが，$R^{2}/c$は$c$の偏角を$\theta$としたときに$-\theta$の偏角を持つため，反時計回りの回した分を元に戻す必要があります。$c$の共役をとれば元の場所に戻るため，結局
c^{\ast} &= \frac{R^{2}}{\overline{c}}
\end{align}
となります。この関係を「反転像」と呼ぶことにします。これを先ほどの問題にこの関係を適用すれば，$-2i$の反転像が$-1/c$となるため，
-\frac{1}{c}= \frac{1}{\overline{2i}} = -\frac{1}{2i}
\end{align}
が得られます。これを解くと$c=2i$が得られます。
補足2
例題は両辺を二乗することでも解けます。実際，
(iz+2)(-i\overline{z}+2) = (cz+1)(-\overline{c}\overline{z}+2)
\end{align}
より
5+(2iz-2i\overline{z}) = (|c|^{2}+1)+(cz+\frac{\overline{c}}{z})
\end{align}
が得られるため，$z$および$\overline{z}$の係数を比較すると$c-2i$が得られます。これは$|c|^{2}+1=5$を満たすため適切です。
コメント