本記事は機械学習の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
PCAとは
PCAは情報を圧縮するための手法の1つです。複雑なデータよく表すことのできる情報の軸(主成分)をうまく抽出することで,効率的に多変量データの特徴を扱うことを可能にします。多重共線性でお伝えしている重回帰分析とは異なり,データの予測を目的とする手法ではないため,データに説明変数や目的変数といったような区別がつかないことにも注意してください。
PCAは複雑な情報の特徴をうまく捉えるための判断基準を決めてくれる手法だと考えておきましょう。機械学習との関連として,オートエンコーダが主成分分析の非線形拡張であることは有名です。
定式化
以下ではPCAの定式化を確認します。
問題設定
前述の通り,PCAは多変量解析で重宝する手法の1つです。多変量のデータ$\mX$を「主成分」と呼ばれる変数$\mP$の線型結合で表します。
\mX &= \mS\mP^T \\[0.7em]
&= \sum_{r=1}^{R}\vs_r \vp_r^T \label{eq:1}
\end{align}
ただし,$R$は$\mX$の階数,$\mP$は主成分ベクトルを列にもつ主成分行列(ローディング行列とも呼ばれますがここでは分かりやすさを重視して主成分行列と呼ぶことにします),$\mS$は主成分$\mP$がどれだけ影響しているかの度合いを表すスコア(係数)です。
階数は採用できる主成分の個数に相当します。後で見るように,PCAは固有値問題と密接な関係があり,それゆえ行列の階数が採用できる主成分の個数に効いてくるという訳です。
式(\ref{eq:1})を要素ごとに書き下してみましょう。データ行列$\mX$は$D$次元のデータ$N$サンプルからなります。
\begin{bmatrix}
x_{11} & x_{12} & \cdots & x_{1 D} \\
x_{21} & x_{22} & \cdots & x_{2 D} \\
\vdots & \vdots & \ddots & \vdots \\
x_{N 1} & x_{N 2} & \cdots & x_{N D}
\end{bmatrix}
&=
\sum_{r=1}^{R}
\begin{bmatrix}
s_{r1} \\
\vdots \\
s_{rN}
\end{bmatrix}
\begin{bmatrix}
p_{r1} \ldots p_{rD}
\end{bmatrix}\\[0.7em]
&=
\text{行列1} + \text{行列2} + \ldots + \text{行列R}
\end{align}
この式から,PCAはデータ行列を複数の行列の和で表そうとする手法であることが分かります。これは,ベクトル形式で書き直すと分かりやすいです。
\begin{bmatrix}
\vx_1 \\
\vdots \\
\vx_N
\end{bmatrix}
&=
\sum_{r=1}^{R}
\begin{bmatrix}
\vx_{1}^{(r)} \\
\vdots \\
\vx_{N}^{(r)}
\end{bmatrix}
\end{align}
ただし,$\vx_{n}^{(r)}$は以下のようにおきました。
\vx_{n}^{(r)} &=
\begin{bmatrix}
s_{nr}p_{n1} \cdots s_{nr}p_{nD}
\end{bmatrix}
\end{align}
$N$サンプルの$D$次元データをそれぞれ$R$個の同じ大きさのベクトルの和で表そうとしています。例えば,データ$\vx_{n}$の$d$次元目をみてみましょう。
x_{nd} &= \sum_{r=1}^{R} x_{nd}^{(r)} \\[0.7em]
&= s_{n1}p_{nd} + \ldots + s_{nR}p_{nd}
\end{align}
このように,元のデータが主成分ベクトルの要素の線形和として表されていることが分かります。しかし,式($\ref{eq:1}$)では$\mX$というデータ(情報)を圧縮していることにはなりません。そこで,PCAでは大事な主成分ベクトルを上から$D'$個使うことでデータ$\mX$の特徴を抽出します。
\mX &= \mS\mP^T \\[0.7em]
&= \sum_{m=1}^{D'}\vs_m \vp_m^T + \mE \label{eq:2}\\[0.7em]
&= (\text{行列1} + \text{行列2} + \ldots + \text{行列$D'$}) + \text{埋め合わせの行列} \\[0.7em]
&= \text{圧縮された情報} + \text{残差}
\end{align}
ただし,$\mE$は元データと圧縮されたデータの残差を表します。PCAの問題設定は,式($\ref{eq:2}$)にそうような形で主成分ベクトル$\vp$とスコア$\vs$を見つけ出すことです。言い換えれば,PCAの目的は$\vp$と$\vs$をデータを元に計算することです。ここで,式(\ref{eq:2})の右辺に登場する$\vs_m \vp_m^T$を主成分と呼ぶことにします。例えば,$m$番目の主成分は$m$番目の主成分ベクトルによって抽出されたデータを表します。
正規直交基底への正射影
少々天下り的ですが,PCAは正規直交基底への正射影です。PCAでは主成分ベクトルを互いに直交するように選びます。主成分ベクトルが正規化されている前提に立てば,主成分ベクトルは正規直交基底になります。
つまり,データを主成分ベクトルの線形和で表すということは,データを正規直交基底上で表していることに他なりません。このとき,係数であるスコアは各基底における座標(データを各規定に正射影したときの原点からのキョリ)を表します。これらの考察から,PCAに関して重要な考察が得られます。
PCAにおける主成分ベクトルは(正規)直交基底をなし,スコア(係数)は基底上の座標を表します。すなわち,PCAは主成分ベクトルへの正射影問題と捉えることができます。
なお,PCAでは元のデータに標準化(平均0,分散1となるようデータを整形する操作)を施す前処理を行います。この処理はオートスケーリングと呼ばれ,データの各次元が異なる単位系(例えばcmとkgなど)を用いている場合でも,値の大小やデータの散らばりに影響を受けることなくPCAを行うことができます。
固有値問題とのつながり
主成分ベクトルは,データをよく表せるような基底であることが望ましいです。そこで,PCAでは以下の2つの方針に則って主成分を計算していきます。
- 正射影後のデータの分散が最大になる
- 正射影前後のデータの二乗誤差を最小にする
以下では,これらの2通りの方針について,どちらも固有値問題に帰着することを示します。まずは,両方針に共通して元のデータと射影後のデータを数学的に表現しておきましょう。射影先のベクトルの1つ$\vu$,つまり主成分ベクトルを正規化したベクトルの1つは以下のように設定します。
\vu &= [u_1 u_2 \cdots u_d]^T\\[0.7em]
\end{align}
ただし,$\vu$は以下を満たします。
|\vu| &= 1
\end{align}
$\vu$は$d$次元のベクトルですが,$\vu$上に射影した場合には$d$次元上の1点になってしまうことに注意です。簡単のため,最初は$1$点への射影について考え,そのあとに多次元に拡張したいと思います。さて,$d$次元$N$サンプルの対象のデータ$\mX$を用いて,射影前の各種統計量は以下のように表されます。
\boldsymbol{\mu} &= \frac{1}{N}\sum_{n=1}^{N} \mX_n \\[0.7em]
\Sigma &= \frac{1}{N} \sum_{n=1}^{N} (\mX_n - \boldsymbol{\mu})(\mX_n - \boldsymbol{\mu})^T
\end{align}
$\vu$上へ射影されたデータは,内積で表される$d$次元空間の点になります。これを利用して,以下のようにして射影後の各種統計量を求めます。まずは,$\hat{\vmu}$です。
\hat{\vmu} &= \frac{1}{N}\sum_{n=1}^{N} \vu^T \mX_n \\
&= \vu^T \frac{1}{N}\sum_{n=1}^{N} \mX_n \\
&= \vu^T \boldsymbol{\mu}\quad (\text{スカラー})
\end{align}
続いて,$\hat{\Sigma}$です。
\hat{\Sigma} &= \frac{1}{N} \sum_{n=1}^N (\vu^T \mX_n - \vu^T \boldsymbol{\mu}) (\vu^T \mX_n - \vu^T \boldsymbol{\mu})^T\\
&= \vu^T \Sigma \vu\quad (\text{スカラー})
\end{align}
ここから,各方針に枝分かれしていきます。
1.の方針
$|\vu|= \vu^T \vu = 1$という条件下で$\vu^T {\Sigma}\vu$を最大にすればOKです。条件付きの最大最小問題ですので,ラグランジュの未定乗数法を利用しましょう。目的関数は以下になります。
L(\vu, \lambda)
&= \vu^T \boldsymbol{\Sigma}\vu - \lambda(\vu^T \vu)
\end{align}
目的関数の導関数を$0$にする$\vu$を求めます。
\frac{\partial L}{\partial \vu}
&= ({\Sigma} + {\Sigma}^T)\vu - \lambda (\bf{I} + \bf{I}^T)\vu\\
&= 2({\Sigma}\vu - \lambda\vu)\\
&= 0
\end{align}
すなわち,以下が成り立ちます。
{\Sigma} \vu &= \lambda\vu
\end{align}
この式を少しいじることで,$\lambda$に意味づけをしてあげましょう。
\vu^T {\Sigma}\vu = \lambda = \hat{\Sigma}
\end{align}
つまり,$\lambda$は射影後の分散そのものだということです。とても大切な事実です。つまり,$\vu$は${\Sigma}$の最大固有値$\lambda$に対する固有ベクトルになります。なぜ最大なのかというと,今回の目的が射影後の分散$\lambda$を最大にすることが目的だったからです。
これを,$2$次元上への射影に拡張する場合は,新しい射影上のベクトル$\vu_2$が$\vu_1=\vu$に直交するという条件をつけて全く同じ議論を行えばOKです。すると,射影後の分散は大きい順に選ばれていきますので,できあがる正規直交基底$(\vu_1, \vu_2, \cdots, \vu_{D'})$は,${\Sigma}$の固有値を大きい順に並べた$(\lambda_1, \lambda_2, \cdots, \lambda_{D'})$に対応する固有ベクトルとして与えられることが示ました。
先ほど$\mX$の階数が採用できる主成分の数に相当するとお伝えしましたが,その根拠がここで示した内容です。主成分ベクトルは固有値に対応する固有ベクトルですので,存在する固有値の個数が採用できる主成分の個数に相当します。一般に,行列$\mX$の階数を$R$,重複も含めた0でない固有値の個数を$N(R)$とおけば,$R\geq N(R)$が成り立つので,データ行列の階数が$R$のときは重複を許して最大でも$R$個の主成分ベクトルを選ぶことができるという訳です。
2.の方針
こちらの方針では,$\vu$上に正射影したデータが$(\vu^T \mX_n)\vu$と現れることを利用します。これは,内積$\vu^T \mX_n$が正射影後の空間におけるデータの「長さ」を表していることを考えれば分かります。今回の目的はデータの射影前後の二乗誤差を最小にすることでした。実際に,二乗誤差を計算してみましょう。
\epsilon^2 &= \sum_{n=1}^{N} |\mX_n - (\vu^T \mX_n)\vu |^2\\[0.7em]
&= \sum_{n=1}^{N} \bigl( \mX_n - (\vu^T \mX_n)\vu \bigr)^T \bigl( \mX_n - (\vu^T \mX_n)\vu \bigr)\\[0.7em]
&= \sum_{n=1}^N \bigl( \mX_n^T \mX_n - 2|\vu^T \mX_n|^2 + |\vu^T \mX_n|^2 \bigr)\\[0.7em]
&\propto \sum_{n=1}^N - |\vu^T \mX_n|^2 \quad (\because \text{$\mX_n^T \mX$は常に一定})
\end{align}
この式をよく眺めてみましょう。「変換後データの分散値の$-N$倍」になっていることが分かりますでしょうか。つまり,変換後データの分散値が$\bf{u^T }\Sigma \vu$であることに注意すれば,以下の関係式が成立します。
\epsilon^2 &= -N \bf{u^T}\Sigma \vu
\end{align}
1.の方針は変換後データの分散$\bf{u^T }\Sigma \vu$の最大化,2.の方針は二乗誤差$\epsilon^2$の「最小化」でしたので,上の式より両者が等価であることが分かります。以上より,どちらの方針にしても,主成分分析は分散共分散行列の固有値問題に帰着することが示ました。
ちなみに,正規化した固有ベクトルを並べた行列を$\mU$とおけば,$\mU$が主成分行列$\mP$に対応することに注意して以下の関係式を用いれば,スコアを計算することができます。
\mX &= \mS \mU^T \\[0.7em]
\mS &= \mX \mU\label{eq:score}
\end{align}
元のデータを表す軸は主成分分析によって固有ベクトル方向に変換されます。なぜなら,元のデータを表す軸は単位行列であり,以下のように計算できるからです。
\mI \mU &= \mU
\end{align}
次元数$D'$の選び方
さて,PCAの目的は情報の圧縮でした。そのためには,行列のランクよりも小さい次元$D'$を選び,その数だけ用意した主成分ベクトルで元のデータ$\mX$を選ぶ必要がありました。そこで,$D'$はどのようにして選べば良いのでしょうか。
この答えは自明ではありません。しかし,参考になる指標が存在します。それは「寄与率」と呼ばれる指標であり,各主成分がどれだけ元のデータを表しているかを示します。
PCAのモチベーションとして「データをどれだけよく表しているか」の指標に対して分散を持ち出しました。そのため,寄与率は分散を用いて以下のように定義されます。
\text{$i$番目の主成分の寄与率} &= \frac{i\text{番目の分散}}{0\text{番目の分散}+\cdots R \text{番目の分散}}
\end{align}
寄与率の意味は,データ全体の散らばり具合に占める特定の主成分の散らばり具合です。先ほどもお伝えしましたが,データの散らばり具合が「データをどれだけよく表しているか」でしたので,このような定義が用いられています。さて,先ほどの議論より$i$番目の分散は$i$番目に大きい固有値$\lambda_i$でした。これを用いて寄与率の定義を書き換えてみます。
\text{$i$番目の主成分の寄与率} &= \frac{\lambda_i}{\sum_{j=1}^{R}\lambda_j}
\end{align}
また,分散共分散行列$\Sigma$の対角成分が各サンプルの分散であることから,寄与率は最終的に以下のようにも書き換えられます。
\text{$i$番目の主成分の寄与率} &=\frac{\lambda_i}{\mathrm{trace}[V]}
\end{align}
この寄与率をウォッチしながら$D'$を決めていきます。具体的には,累積寄与率をみながら$D'$を徐々に増やしていけば良いです。
アルゴリズム
PCAの定式化を確認したところで,実際にPCAを行う際のアルゴリズムを確認しておきましょう。
- $D$次元$N$サンプルのデータ$\mX$を用意
- 各特徴量に対して平均0,分散1となるよう標準化
- 分散共分散行列の固有値問題を解く
- 累積寄与率をウォッチしながら$D'$を決める
- 可視化などにより考察を行う
具体例
本記事では,全国各地の日本酒の志向をPCAを用いて分析していきたいと思います。
データ作成
以下では全国各地の日本酒(清酒)を都道府県別に分けたときに,どのような考察が得られるかをみていきます。データは国税庁の「全国市販酒類調査の結果について(平成25年度調査分)」の表9より一部抜粋しました。
普通酒の定義は「特定名称清酒以外の清酒」です。特定名称清酒は醸造アルコールの有無と精米歩合によって以下の8種類に分類されています。国税庁によると,日本酒は一般酒と特定名称清酒に分けられます(「清酒の製法品質表示基準」の概要より)。
- 吟醸酒
- 大吟醸酒
- 純米酒
- 純米吟醸酒
- 純米大吟醸酒
- 特別純米酒
- 本醸造酒
- 特別本醸造酒
今回は,これらの特定名所清酒以外の清酒である普通酒を対象とします。清酒を表す特徴量は,以下の7点($D=7$)です。
- アルコール分(アルコール度数)
- 日本酒度(清酒の比重・糖分の含有量)
- エキス分(100ml中に含まれる不揮発性分)
- 酸度(有機酸の含有量)
- アミノ酸度(アミノ酸の含有量)
- 甘辛度(日本酒度と酸度から算出)
- 濃淡度(日本酒度と酸度から算出)
※日本酒度が低ければ低いほど純粋な水よりも重いことを表しているためエキス分(糖分)がたくさん含まれていることを示す
この指標を見ると,日本酒度がエキス分の含有量を暗に表していることや,甘辛度と濃淡度は日本酒度と酸度から算出していることから,PCAを適用すればより適切で少数の指標を用いてデータを表せる可能性が示唆されます。今回は,対象とする地域として以下の9地点を選びました。
- 札幌
- 仙台
- 関東信越
- 金沢
- 名古屋
- 大阪
- 広島
- 高松
- 福岡
- 熊本・沖縄
以下が,上記7地点の特徴量です。
| アルコール分 | 日本酒度 | エキス分 | 酸度 | アミノ酸度 | 甘辛度 | 濃淡度 | |
| 札幌 | 15.47 | 3.6 | 4.55 | 1.22 | 1.05 | -0.15 | -0.89 |
| 仙台 | 15.32 | 3.7 | 4.51 | 1.26 | 1.19 | -0.20 | -0.83 |
| 関東信越 | 15.32 | 5.2 | 4.29 | 1.05 | 1.18 | -0.08 | -1.27 |
| 金沢 | 15.20 | 5.2 | 4.21 | 1.25 | 1.30 | -0.34 | -0.91 |
| 名古屋 | 15.29 | 4.5 | 4.35 | 1.14 | 1.37 | -0.15 | -1.08 |
| 大阪 | 15.39 | 3.4 | 4.66 | 1.23 | 1.28 | -0.15 | -0.83 |
| 広島 | 15.39 | 3.4 | 4.57 | 1.16 | 1.26 | -0.07 | -0.99 |
| 高松 | 15.27 | 4.8 | 4.33 | 1.15 | 1.10 | -0.18 | -1.02 |
| 福岡 | 15.13 | 2.0 | 4.78 | 1.22 | 1.43 | -0.01 | -0.82 |
| 熊本・沖縄 | 15.36 | 1.8 | 4.86 | 1.19 | 1.31 | 0.05 | -0.86 |
単位系がバラバラですので,それぞれの特徴量に関して平均0,分散1となるように標準化を行います。
| アルコール分 | 日本酒度 | エキス分 | 酸度 | アミノ酸度 | 甘辛度 | 濃淡度 | |
| 札幌 | 1.67 | -0.14 | 0.19 | 0.55 | -1.76 | -0.21 | 0.44 |
| 仙台 | 0.06 | -0.05 | 0.00 | 1.21 | -0.51 | -0.70 | 0.88 |
| 関東信越 | 0.06 | 1.26 | -1.08 | -2.27 | -0.60 | 0.47 | -2.35 |
| 金沢 | -1.22 | 1.26 | -1.47 | 1.04 | 0.47 | -2.06 | 0.29 |
| 名古屋 | -0.26 | 0.65 | -0.79 | -0.78 | 1.10 | -0.21 | -0.96 |
| 大阪 | 0.81 | -0.32 | 0.73 | 0.71 | 0.30 | -0.21 | 0.88 |
| 広島 | 0.81 | -0.32 | 0.29 | -0.45 | 0.12 | 0.56 | -0.29 |
| 高松 | -0.47 | 0.91 | -0.88 | -0.61 | -1.32 | -0.51 | -0.51 |
| 福岡 | -1.97 | -1.54 | 1.31 | 0.55 | 1.64 | 1.15 | 0.96 |
| 熊本・沖縄 | 0.49 | -1.72 | 1.70 | 0.05 | 0.56 | 1.73 | 0.66 |
実装
まずは必要なライブラリを用意しましょう。
import scipy.stats
import numpy as np
import numpy.linalg as LA
import matplotlib.pyplot as plt整形前のデータを打ち込みます。本来であればcsvなどを利用して読み込むのが効率的ですが,今回はベタ打ちしてしまおうと思います。
alcohol = [15.47, 15.32, 15.32, 15.20, 15.29, 15.39, 15.39, 15.27, 15.13, 15.36]
nihonshudo = [3.6, 3.7, 5.2, 5.2, 4.5, 3.4, 3.4, 4.8, 2.0, 1.8]
extract = [4.55, 4.51, 4.29, 4.21, 4.35, 4.66, 4.57, 4.33, 4.78, 4.86]
acidity = [1.22, 1.26, 1.05, 1.25, 1.14, 1.23, 1.16, 1.15, 1.22, 1.19]
amino_acidity = [1.05, 1.19, 1.18, 1.30, 1.37, 1.28, 1.26, 1.10, 1.43, 1.31]
salty_sweet = [-0.15, -0.20, -0.08, -0.34, -0.15, -0.15, -0.07, -0.18, -0.01, 0.05]
strong_weak = [-0.89, -0.83, -1.27, -0.91, -1.08, -0.83, -0.99, -1.02, -0.82, -0.86]scipy.statsを利用してデータの標準化を行います。
alcohol_norm = scipy.stats.zscore(alcohol)
nihonshudo_norm = scipy.stats.zscore(nihonshudo)
extract_norm = scipy.stats.zscore(extract)
acidity_norm = scipy.stats.zscore(acidity)
amino_acidity_norm = scipy.stats.zscore(amino_acidity)
salty_sweet_norm = scipy.stats.zscore(salty_sweet)
strong_weak_norm = scipy.stats.zscore(strong_weak)(N, D)のデータ行列を作成します。なお,今回はN=10, D=7です。
X = np.array([alcohol_norm, nihonshudo_norm, extract_norm, acidity_norm, amino_acidity_norm, salty_sweet_norm, strong_weak_norm]).transpose(1,0)データが標準化できているかどうか確かめてみましょう。
m = np.mean(X, axis=0)
S = (1/X.shape[0]) * ((X - m).T @ (X - m))
print(np.round(m,3))
"""
[ 0. -0. -0. 0. -0. 0. -0.]
"""
print(np.round(S, 3))
"""
[[ 1. -0.061 0.174 -0.078 -0.587 0.131 -0.031]
[-0.061 1. -0.984 -0.377 -0.4 -0.741 -0.66 ]
[ 0.174 -0.984 1. 0.336 0.327 0.757 0.634]
[-0.078 -0.377 0.336 1. 0.131 -0.339 0.934]
[-0.587 -0.4 0.327 0.131 1. 0.277 0.211]
[ 0.131 -0.741 0.757 -0.339 0.277 1. -0.006]
[-0.031 -0.66 0.634 0.934 0.211 -0.006 1. ]]
"""しっかりと平均0,分散1に標準化できていることが分かります。さて,PCAでは分散共分散行列$S$の固有値問題を解く必要がありました(固有値問題を解かずにPCAを行う方法もあります)。ここでは,固有値を大きい順に並べて対応する固有ベクトルも併せて返すような関数eigsortを定義したいと思います。
def eigsort(S):
eigv_raw, u_raw = LA.eig(S)
eigv_index = np.argsort(eigv_raw)[::-1]
eigv = eigv_raw[eigv_index]
u = u_raw[:, eigv_index]
return [eigv, u]実際に使っていきます。
[eig, U] = eigsort(S)さて,抽出した主成分の寄与率をウォッチしてみましょう。
all_contribution = 0
for i in range(len(eig)):
contribution = eig[i]/7
all_contribution += contribution
print(f"The {i+1}th contribution: {np.round(contribution*100, 1):4}% (cumulative: {np.round(all_contribution*100, 1):5}%)")出力は以下のようになります。
The 1th contribution: 47.9% (cumulative: 47.9%)
The 2th contribution: 26.1% (cumulative: 74.0%)
The 3th contribution: 21.7% (cumulative: 95.7%)
The 4th contribution: 4.1% (cumulative: 99.7%)
The 5th contribution: 0.2% (cumulative: 99.9%)
The 6th contribution: 0.1% (cumulative: 100.0%)
The 7th contribution: 0.0% (cumulative: 100.0%)この結果から,第2主成分まで採用すれば74%の累積寄与率を達成できることが分かります。第3主成分まで採用すれば95.7%もの累積寄与率を達成できますが,可視化の際に3Dでプロットする必要があるため,今回は第2主成分までを採用します。式(\ref{eq:score})を使って各主成分ベクトル(軸)に対応する係数を計算しておきましょう。
S = X @ Uさて,残すは可視化のみです。まずは,第2主成分までを使ってデータを表現してみましょう。その際,同時に元のデータを表す軸を変換した軸である固有ベクトルも表示すると,各主成分にどの要素が寄与しているのかを目で見て確かめることができます。
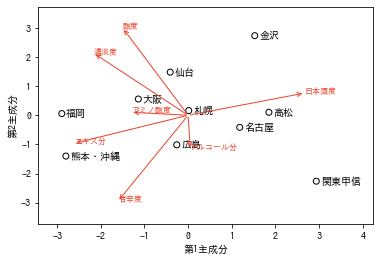
X_list = ["札幌", "仙台", "関東甲信", "金沢", "名古屋", "大阪", "広島", "高松", "福岡", "熊本・沖縄"]
feature_list = ["アルコール分", "日本酒度", "エキス分", "酸度", "アミノ酸度", "甘辛度", "濃淡度"]
plt.rcParams["font.family"] = "IPAGothic"
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_xlim(-np.max(S[:,0])-0.5, np.max(S[:,1])+1.5)
ax.set_ylim(-np.max(S[:,1])-1, np.max(S[:,1])+1)
for i in range(S.shape[0]):
ax.scatter(S[i, 0], S[i, 1], facecolor="None", edgecolors="black")
ax.annotate(X_list[i], xy=(S[i,0]+0.1, S[i, 1]-0.1), family="IPAGothic", size=10)
for i in range(U.shape[0]):
ax.annotate("", xy=(U[i, 0]*5, U[i, 1]*5), xytext=(0, 0), arrowprops=dict(arrowstyle="->", facecolor="#ec442c", edgecolor="#ec442c"))
ax.text(U[i, 0]*5, U[i, 1]*5, feature_list[i], color="#ec442c", family="IPAGothic", size=8)さて,PCAでは抽出した主成分の意味付けが重要でした。今回の第1主成分はほぼ日本酒度に対応していることが分かります。一般に,日本酒度は高ければ高いほど純粋な水に近いことを表しており,いわゆる「辛口度」に対応することが考えられます。他にも「スッキリ度」などと表現しても面白いでしょう。
ここで面白いのが,日本酒度とエキス分がほぼ正反対を向いています。これは,日本酒度が「純粋な水に対してどれだけの糖分(エキス)が含まれているか」という指標を表していることに起因しています。日本酒度が高ければ高いほど,エキス分が少なく純粋な水に近いアッサリした味わいになります。
第2主成分は多くの要因が絡み合っています。中でも,酸度・濃厚度・甘辛度の3指標が大きな影響を与えているようにみえます。酸度は高ければ高いほど濃醇な味わいになること,濃厚度・甘辛度はその名の通り高ければ高いほどそれぞれ濃く・甘く感じます。甘辛度に関しては,第1主成分と少し重複してしまう部分があるため,今回は酸度・濃厚度を採用して第2主成分を「濃醇さ」に対応すると考えます。
改めて,各主成分の名前を書き直してみましょう。
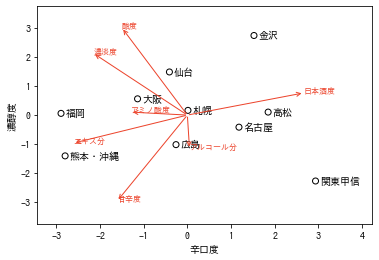
fig = plt.figure()
ax = fig.add_subplot(111, xlabel="辛口度", ylabel="濃醇度")
ax.set_xlim(-np.max(S[:,0])-0.5, np.max(S[:,1])+1.5)
ax.set_ylim(-np.max(S[:,1])-1, np.max(S[:,1])+1)
for i in range(S.shape[0]):
ax.scatter(S[i, 0], S[i, 1], facecolor="None", edgecolors="black")
ax.annotate(X_list[i], xy=(S[i,0]+0.1, S[i, 1]-0.1), size=10)
for i in range(U.shape[0]):
ax.annotate("", xy=(U[i, 0]*5, U[i, 1]*5), xytext=(0, 0), arrowprops=dict(arrowstyle="->", facecolor="#ec442c", edgecolor="#ec442c"))
ax.text(U[i, 0]*5, U[i, 1]*5, feature_list[i], color="#ec442c", size=8)考察
関東甲信は辛口であっさりした味わいのお酒を嗜んでいることが分かります。一方,金沢は辛口寄りであり,非常に濃厚な味わいのお酒を楽しんでいることが分かります。札幌と本州の都市は平均的なお酒を嗜んでいるようです。福岡は甘口なお酒を好む傾向にあるようです。熊本・沖縄は甘口かつあっさりとした味わいのお酒が好きなようです。結局,甘口or辛口,まろやか or スッキリという巷に溢れる日本酒の有名な二つの指標が得られました。この2つの指標の寄与率は75%程度でしたから,三次元に増やすともっと精密な説明軸が得られると考えられます。


コメント